题目内容
在平面直角坐标系 中,点
中,点 ,直线
,直线 经过两点
经过两点 ,
, ,设圆
,设圆 的半径为
的半径为 ,圆心在直线
,圆心在直线 上.
上.
(Ⅰ)求直线 的方程;
的方程;
(Ⅱ) 若圆 被
被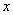 轴截得的弦长为
轴截得的弦长为 ,求圆
,求圆 的方程;
的方程;
(Ⅲ) 若圆 上存在点
上存在点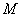 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
解:(Ⅰ)由已知,直线 的斜率
的斜率 ,
,
所以,直线 的方程为
的方程为 .
.
(Ⅱ)因为圆 的圆心在直线
的圆心在直线 上,可设圆心坐标为
上,可设圆心坐标为 ,
,
由已知可得:
所以,圆C方程为: ,或
,或
(Ⅲ)解:∵圆 的圆心在在直线
的圆心在在直线 上,所以,设圆心C为(a,2a-4)
上,所以,设圆心C为(a,2a-4)
则圆 的方程为:
的方程为:
又∵ ∴设M为(x,y)则
∴设M为(x,y)则 整理得:
整理得: 设为圆D
设为圆D
∴点M应该既在圆C上又在圆D上 即:圆C和圆D有交点
∴
由 得
得
由 得
得
终上所述, 的取值范围为:
的取值范围为:

练习册系列答案
相关题目
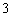 个白球,
个白球,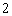 个黑球和1个红球.乙箱子里装有2 个白球,1个黑球和2个红球.这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出3个球,若摸出的6个球中白球个数比黑球多,黑球的个数比红球多,则获奖. (每次游戏结束后将球放回原箱)
个黑球和1个红球.乙箱子里装有2 个白球,1个黑球和2个红球.这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出3个球,若摸出的6个球中白球个数比黑球多,黑球的个数比红球多,则获奖. (每次游戏结束后将球放回原箱)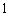 次游戏中,摸出
次游戏中,摸出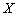 ,求数学期望
,求数学期望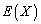 .
. ,直线
,直线 恒过定点
恒过定点 ,则以
,则以 为半径的圆的方程是( )
为半径的圆的方程是( ) B.
B.
 D.
D.
 ,则
,则

 ,则( )
,则( )

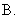

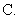

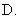


 的对称中心为
的对称中心为 ,记函数
,记函数 的导函数为
的导函数为 ,
, ,则有
,则有 .若函数
.若函数 –
– ,则可求得
,则可求得 +
+ +
+
 +
+ =( )
=( )
 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”; 中,
中, 增加1个单位时,
增加1个单位时, 一定增加2个单位;
一定增加2个单位; 为假命题,则
为假命题,则 均为假命题;
均为假命题; ,使得
,使得 ,则
,则 ,均有
,均有 ;
;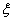 服从正态分布
服从正态分布 ,若
,若 ,则
,则 .
. 是曲线
是曲线 上一点,且在点
上一点,且在点 平行,则点
平行,则点 C.
C. D.
D.