题目内容
15.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与圆(x+1)2+(y-$\sqrt{3}$)2=1相切,则此双曲线的离心率为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
分析 求出圆的圆心与半径,双曲线的渐近线方程,利用渐近线与圆(x+1)2+(y-$\sqrt{3}$)2=1相切,列出方程求解即可.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线bx+ay=0,圆(x+1)2+(y-$\sqrt{3}$)2=1的圆心(-1,$\sqrt{3}$)在的二象限,因为双曲线的渐近线与圆相切,
可得:$\frac{|-b+\sqrt{3}a|}{\sqrt{{b}^{2}+{a}^{2}}}=1$,
可得a=$\sqrt{3}b$,即a2=3b2=3c2-3a2
可得$\frac{{c}^{2}}{{a}^{2}}=\frac{4}{3}$,$\frac{c}{a}$=$\frac{2\sqrt{3}}{3}$.
故选:A.
点评 本题考查双曲线的简单性质的应用,圆锥曲线与圆的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
6.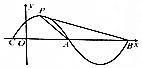 函数y=sin($\frac{π}{2}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象如图所示,其中P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )
函数y=sin($\frac{π}{2}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象如图所示,其中P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )
 函数y=sin($\frac{π}{2}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象如图所示,其中P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )
函数y=sin($\frac{π}{2}$x+φ)(|φ|<$\frac{π}{2}$)的部分图象如图所示,其中P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
3.为了得到函数y=2sin(2x-$\frac{π}{3}$)的图象,只需把函数y=2sinx(2x+$\frac{π}{6}$)的图象上所有的点( )
| A. | 向左平行平移$\frac{π}{2}$个单位长度 | B. | 向右平行平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平行平移$\frac{π}{2}$个单位长度 | D. | 向左平行平移$\frac{π}{4}$个单位长度 |
5.阅读如下程序框图,如果输出i=1008,那么空白的判断框中应填入的条件是( )

| A. | S<2014 | B. | S<2015 | C. | S<2016 | D. | S<2017 |
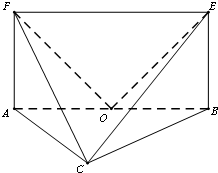 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.