题目内容
7.已知下列命题:①有两个侧面是矩形的四棱柱是直四棱柱;
②若一个三棱锥三个侧面都是全等的等腰三角形,则此三棱锥是正三棱锥;
③已知f(x)的定义域为[-2,2],则f(2x-3)的定义域为[1,3];
④设函数y=f(x)定义域为R,则函数y=f(1-x)与y=f(x-1)的图象关于直线x=1对称;
⑤已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x≤2}\\{-\frac{1}{2}x+2,x>2}\end{array}\right.$,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是(2,4)
其中正确的是④⑤.(填上所有正确命题的序号)
分析 ①,当两个侧面是矩形且相邻时,四棱柱是直四棱柱;当两个侧面是矩形且不相邻时,四棱柱不是直四棱柱;
②,侧面都是等腰三角形的三棱锥不一定是正三棱锥;
③,-2≤2x-3≤2⇒$\frac{1}{2}$≤x≤$\frac{5}{2}$,则f(2x-3)的定义域为[$\frac{1}{2}$,$\frac{5}{2}$],
④,函数y=f(-x)与y=f(x)的图象关于直线x=0对称,则函数y=f(1-x)=f(-(x-1))与y=f(x-1)的图象关于直线x=1对称
⑤,画出函数的图象,根据a,b,c互不相等,且f(a)=f(b)=f(c),我们令a<b<c,我们易根据对数的运算性质,及c的取值范围得到abc的取值范围
解答 解:对于①,当两个侧面是矩形且相邻时,四棱柱是直四棱柱;当两个侧面是矩形且不相邻时,四棱柱不是直四棱柱,故①错;
对于②侧面都是等腰三角形的三棱锥不一定是正三棱锥,
如图所示,VA=VC=BC=AB,AC=VB时,不一定是正三棱锥,故错;
对于③,∵-2≤2x-3≤2⇒$\frac{1}{2}$≤x≤$\frac{5}{2}$,则f(2x-3)的定义域为[$\frac{1}{2}$,$\frac{5}{2}$],故错;
对于④,函数y=f(-x)与y=f(x)的图象关于直线x=0对称,则函数y=f(1-x)=f(-(x-1))与y=f(x-1)的图象关于直线x=1对称,故正确;
对于⑤,若a,b,c互不相等,且f(a)=f(b)=f(c),令a<b<c,则a•b=1,2<c<4,故2<abc<4,故正确;
故答案为:④⑤
点评 本题考查了命题真假的判定,涉及到了大量的基础知识,属于基础题.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
17.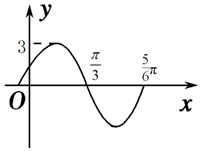 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )| A. | f(x)的一个对称中心为$(\frac{4π}{3},0)$ | B. | f(x)的图象关于直线$x=-\frac{1}{12}π$ 对称 | ||
| C. | f(x)在$[-π,-\frac{π}{2}]$上是增函数 | D. | f(x)的周期为$\frac{π}{2}$ |
15.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与圆(x+1)2+(y-$\sqrt{3}$)2=1相切,则此双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
2.三个数a=0.65,b=50.6,c=log0.65,则a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
12.设a,b是非零实数,若a>b,则一定有( )
| A. | $a+\frac{1}{b}>b+\frac{1}{a}$ | B. | $\frac{1}{{a{b^2}}}>\frac{1}{{{a^2}b}}$ | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | ab>b2 |