题目内容
函数y=f（x）在[1，2]连续，若f（1）＞0，f（2）＜0，则f（x）在（1，2）上零点的个数为________．
证明：∵函数y=f（x）在[1，2]连续，且f（1）＞0，f（2）＜0，
由函数的零点判定定理可知，f（x）在[1，2]上至少有一个零点．
故答案为：至少有一个．
分析：先根据函数在[1，2]上的连续性，然后结合f（1）＞0，f（2）＜0，依据零点判定定理即可判断．
点评：本题主要考查了函数的零点判定定理的简单应用，属于基础试题．
由函数的零点判定定理可知，f（x）在[1，2]上至少有一个零点．
故答案为：至少有一个．
分析：先根据函数在[1，2]上的连续性，然后结合f（1）＞0，f（2）＜0，依据零点判定定理即可判断．
点评：本题主要考查了函数的零点判定定理的简单应用，属于基础试题．
练习册系列答案
相关题目
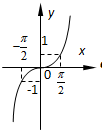已知函数y=f（x）的图象如图，则函数
