��Ŀ����
13����֪Բ����$C��\left\{{\begin{array}{l}{x=2cos��}\\{y=sin��}\end{array}}\right.����Ϊ������$�Ͷ���$A��{0��\sqrt{3}}��$��F1��F2�Ǵ�Բ���ߵ����ҽ��㣬��ԭ��OΪ���㣬��x���������Ϊ���Ὠ��������ϵ��������ֱ��AF2�ļ����귽�̣�
��������F1����ֱ��AF2��ֱ��ֱ��l����Բ������M��N���㣬��||MF1|-|NF1||��ֵ��
���� ������ȥ�������ɵ�����C�ķ���Ϊ$\frac{{x}^{2}}{4}$+y2=1���ȵ�ֱ�ߵ���ͨ���̣���Ϊ�����귽�̼��ɣ�
������l�ķ��̣��ⷽ����ɵý������꣬�������ľ��빫ʽ�ɵã�
��� �⣺������ȥ�������ɵ�����C�ķ���Ϊ$\frac{{x}^{2}}{4}$+y2=1��
�ɵ�F1��-$\sqrt{3}$��0����F2��$\sqrt{3}$��0����
��ֱ��AF2��б��Ϊk=$\frac{\sqrt{3}-0}{0-\sqrt{3}}$=-1��
��ֱ�߷���Ϊy-$\sqrt{3}$=-��x-0������x+y=$\sqrt{3}$��
�༫���귽��Ϊ��cos��+��sin��=$\sqrt{3}$��
��������F1��-$\sqrt{3}$��0������ֱ��AF2��ֱ��ֱ��lб��Ϊ1��
��l�ķ���Ϊy-0=x+$\sqrt{3}$����y=x+$\sqrt{3}$��
����$\left\{\begin{array}{l}{y=x+\sqrt{3}}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$�ɽ��M��$\frac{-4\sqrt{3}+2\sqrt{2}}{5}$��$\frac{\sqrt{3}+2\sqrt{2}}{5}$����N��$\frac{-4\sqrt{3}-2\sqrt{2}}{5}$��$\frac{\sqrt{3}-2\sqrt{2}}{5}$����
���������ľ��빫ʽ�ɵ�||MF1|-|NF1||=$\frac{8}{5}$��
���� ���⿼����Բ�IJ������̺�ֱ�ߵļ����귽�̣��漰ֱ�ߺ���Բ�ཻ�����⣬���е��⣮

 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�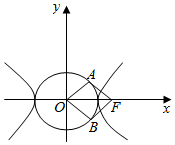 ��֪˫���߷���$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$����OΪԲ�ģ�ʵ���᳤Ϊ�뾶��ԲO����˫���ߵĽ���F��ԲO���������ߣ��е�ΪA��B�����ı���FAOBΪ�����Σ���˫���ߵ�������Ϊ��������
��֪˫���߷���$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��a��0��b��0��$����OΪԲ�ģ�ʵ���᳤Ϊ�뾶��ԲO����˫���ߵĽ���F��ԲO���������ߣ��е�ΪA��B�����ı���FAOBΪ�����Σ���˫���ߵ�������Ϊ��������| A�� | $\frac{3}{2}$ | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | 2 |
| A�� | $[{\frac{��}{6}��\frac{5��}{6}}]$ | B�� | $��{\frac{��}{6}��\frac{5��}{6}}��$ | C�� | $��{\frac{��}{6}��\frac{��}{2}}���ȣ�{\frac{��}{2}��\frac{5��}{6}}��$ | D�� | $[{\frac{��}{6}��\frac{��}{2}}���ȣ�{\frac{��}{2}��\frac{5��}{6}}]$ |
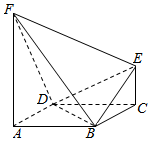 ��ͼ���ڼ�����ABCDEF�У�FA��ƽ��ABCD��EC��FA��FA=2EC=2$\sqrt{2}$������ABCDΪƽ���ı��Σ�AD��BD��AD=BD=2��FD��BE��
��ͼ���ڼ�����ABCDEF�У�FA��ƽ��ABCD��EC��FA��FA=2EC=2$\sqrt{2}$������ABCDΪƽ���ı��Σ�AD��BD��AD=BD=2��FD��BE��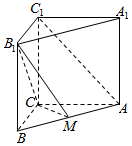 ��ͼ��ֱ������ABC-A1B1C1�У�AC=4��BC=3��AA1=4��AC��BC����M���߶�AB�ϣ�
��ͼ��ֱ������ABC-A1B1C1�У�AC=4��BC=3��AA1=4��AC��BC����M���߶�AB�ϣ� ��֪����̨ABCD-A1B1C1D1�����µ���ֱ��DZ߳�Ϊ2��4�������Σ�AA1=4��AA1�͵���ABCD����PΪDD1���е㣮
��֪����̨ABCD-A1B1C1D1�����µ���ֱ��DZ߳�Ϊ2��4�������Σ�AA1=4��AA1�͵���ABCD����PΪDD1���е㣮 ��ͼ��ʾ������S-ABCD�У�����ABCDΪ�����Σ���AB=4��SA��ƽ��ABCD����SDA=60�㣬E��F��G�ֱ���SC��SD��AC�ϵĵ㣬��$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$��
��ͼ��ʾ������S-ABCD�У�����ABCDΪ�����Σ���AB=4��SA��ƽ��ABCD����SDA=60�㣬E��F��G�ֱ���SC��SD��AC�ϵĵ㣬��$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$��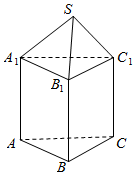 ��ͼ��ʾ�ļ���������һ��������S-A1B1C1��һ�������ⳤ����ȵ���������ABC-A1B1C1��϶��ɣ��Ҹü�������������������ж��㶼�ڸ������ϣ��ı����Ϊ7�У�������S-A1B1C1�����Ϊ$\frac{\sqrt{21}-3}{8}$��
��ͼ��ʾ�ļ���������һ��������S-A1B1C1��һ�������ⳤ����ȵ���������ABC-A1B1C1��϶��ɣ��Ҹü�������������������ж��㶼�ڸ������ϣ��ı����Ϊ7�У�������S-A1B1C1�����Ϊ$\frac{\sqrt{21}-3}{8}$��