题目内容
若函数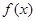 的导函数
的导函数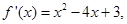 则函数
则函数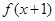 的单调递减区间是( )
的单调递减区间是( )
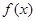 的导函数
的导函数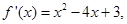 则函数
则函数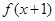 的单调递减区间是( )
的单调递减区间是( ) A.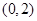 | B.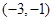 | C.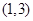 | D.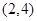 |
A
试题分析:由
 <0得,
<0得, ,所以,函数
,所以,函数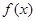 的减区间为(1,3);又函数
的减区间为(1,3);又函数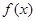 的的图像向左平移1个单位即得到函数
的的图像向左平移1个单位即得到函数 的图象,所以,函数
的图象,所以,函数 的单调递减区间是(0,2),选A。
的单调递减区间是(0,2),选A。点评:简单题,在某区间,导数非负,函数为增函数,导数非正,函数为减函数。

练习册系列答案
相关题目
题目内容
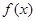 的导函数
的导函数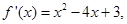 则函数
则函数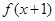 的单调递减区间是( )
的单调递减区间是( ) A.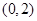 | B.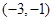 | C.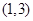 | D.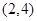 |
 <0得,
<0得, ,所以,函数
,所以,函数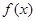 的减区间为(1,3);又函数
的减区间为(1,3);又函数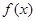 的的图像向左平移1个单位即得到函数
的的图像向左平移1个单位即得到函数 的图象,所以,函数
的图象,所以,函数 的单调递减区间是(0,2),选A。
的单调递减区间是(0,2),选A。