题目内容
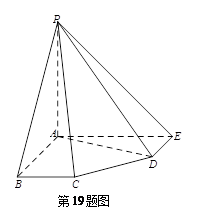
(本题满分12分)在五棱锥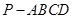 ,
,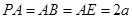 ,
,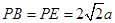 ,
,
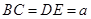 ,
,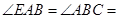
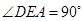 ,
,
(1)求证: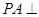 平面
平面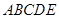 ;
;
(2)求二面角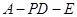 的正弦值.
的正弦值.
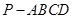 ,
,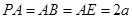 ,
,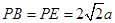 ,
,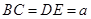 ,
,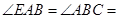
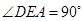 ,
,(1)求证:
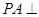 平面
平面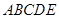 ;
;(2)求二面角
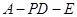 的正弦值.
的正弦值.
(2)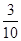
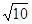
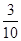
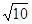
(1)由已知条件根据勾股定理证明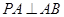 ,
,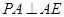 ,再由直线垂直平面的判定定理证明.(2)先作出二面角的平面角,通过相似三角形对应边成比例求解.
,再由直线垂直平面的判定定理证明.(2)先作出二面角的平面角,通过相似三角形对应边成比例求解.
试题分析:(1)在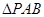 中,
中,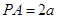 ,
,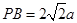 ,
,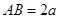 ,
,
∴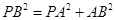 ,∴
,∴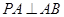 ,
,
同理可证: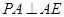 ,
,
又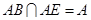 ,
,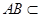 平面
平面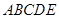 ,
,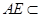 平面
平面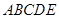 ,
,
∴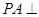 平面
平面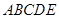 . ……6分
. ……6分
(2)过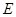 作
作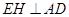 于
于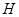 ,
,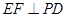 于
于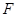 ,则
,则 平面
平面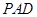 ,
,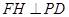 ,
,
∴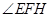 为二面角
为二面角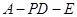 的平面角. ……8分
的平面角. ……8分
又在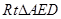 和
和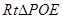 中,
中,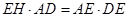 ,
,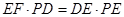 ,
,
∴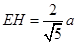 ,
,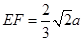 ,∴
,∴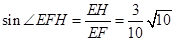 .
.
故二面角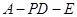 的正弦值为
的正弦值为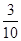
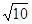 ……12分
……12分
点评: 证明空间中的线面关系一般是转化为平面上的线线关系求解,求解二面角的问题一般用定义法或向量法.用定义法必须找到二面角的平面角.用向量法的关键是建立恰当的空间直角坐标系.
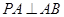 ,
,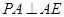 ,再由直线垂直平面的判定定理证明.(2)先作出二面角的平面角,通过相似三角形对应边成比例求解.
,再由直线垂直平面的判定定理证明.(2)先作出二面角的平面角,通过相似三角形对应边成比例求解.试题分析:(1)在
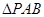 中,
中,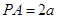 ,
,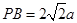 ,
,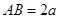 ,
,∴
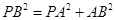 ,∴
,∴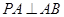 ,
,同理可证:
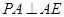 ,
,又
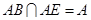 ,
,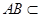 平面
平面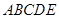 ,
,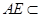 平面
平面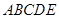 ,
,∴
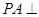 平面
平面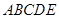 . ……6分
. ……6分 (2)过
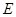 作
作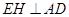 于
于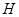 ,
,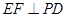 于
于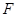 ,则
,则 平面
平面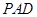 ,
,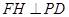 ,
,∴
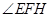 为二面角
为二面角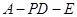 的平面角. ……8分
的平面角. ……8分又在
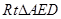 和
和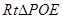 中,
中,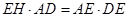 ,
,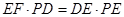 ,
,∴
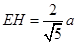 ,
,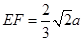 ,∴
,∴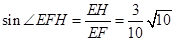 .
.故二面角
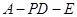 的正弦值为
的正弦值为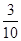
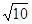 ……12分
……12分点评: 证明空间中的线面关系一般是转化为平面上的线线关系求解,求解二面角的问题一般用定义法或向量法.用定义法必须找到二面角的平面角.用向量法的关键是建立恰当的空间直角坐标系.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 的图象是连续不断的曲线,且有如下的对应值表
的图象是连续不断的曲线,且有如下的对应值表

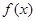 的导函数
的导函数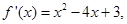 则函数
则函数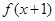 的单调递减区间是( )
的单调递减区间是( ) 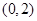
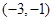
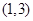
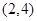
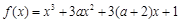 有极大值和极小值,则
有极大值和极小值,则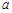 的取值范围是__ .
的取值范围是__ .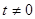 ,点P(
,点P(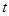 ,0)是函数
,0)是函数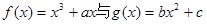 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.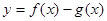 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求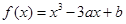 在点
在点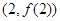 处与直线
处与直线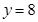 相切,则
相切,则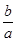 为 .
为 .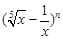 的展开式中,第4项是常数项,则
的展开式中,第4项是常数项,则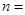
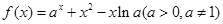 .
.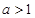 时,求证:函数
时,求证:函数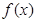 在
在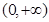 上单调递增;
上单调递增;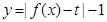 有三个零点,求
有三个零点,求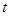 的值;
的值;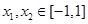 ,使得
,使得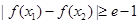 ,试求
,试求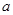 的取值范围。
的取值范围。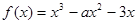 .
.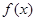 在
在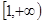 上是增函数,求实数
上是增函数,求实数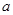 的取值范围;
的取值范围;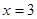 是
是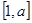 上的最小值和最大值.
上的最小值和最大值.