题目内容
【题目】双曲线
的一个焦点
恰好与抛物线
的焦点重合，且两曲线的一个交点为
，若
，则双曲线的方程为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
求出抛物线的焦点坐标，可得双曲线的焦距，得到
关系式，由
，利用抛物线的焦半径公式求出
的坐标，把点代入双曲线方程，可求得的值，从而可求出双曲线的标准方程．
∵抛物线y2＝8x的焦点F（2，0），
∴由题意知双曲线
1（a＞0，b＞0）的一个焦点为F（2，0），
∴a2+b2＝4，
∵P是抛物线与双曲线的一个交点，|PF|＝5，
∴P点横坐标满足
，代入抛物线y2＝8x得P（3，±2
），
把P（3，±2）代入双曲线1（a＞0，b＞0）得
，
整理得a4﹣37a2+36＝0，
解得a2＝1，或a2＝36（舍）
则b2＝3，
所求双曲线方程为：x2
1．
故选D．
练习册系列答案
相关题目
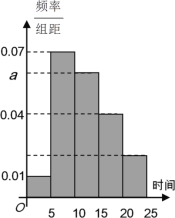
【题目】某保险公司有一款保险产品的历史收益率（收益率
利润
保费收入）的频率分布直方图如图所示：
（1）试估计这款保险产品的收益率的平均值；
（2）设每份保单的保费在20元的基础上每增加
元，对应的销量为
（万份）．从历史销售记录中抽样得到如下5组
与
的对应数据：
| 25 | 30 | 38 | 45 | 52 |
销量为 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
由上表，知
与
有较强的线性相关关系，且据此计算出的回归方程为
．
（ⅰ）求参数
的值；
（ⅱ）若把回归方程
当作
与
的线性关系，用（1）中求出的收益率的平均值作为此产品的收益率，试问每份保单的保费定为多少元时此产品可获得最大利润，并求出最大利润．注：保险产品的保费收入
每份保单的保费
销量．
