题目内容
【题目】已知直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
![]() 若直线
若直线![]() 垂直平分弦
垂直平分弦![]() ,求实数
,求实数![]() 的值;
的值;
![]() 已知点
已知点![]() ,在直线
,在直线![]() 上(
上(![]() 为圆心),存在定点
为圆心),存在定点![]() (异于点
(异于点![]() ),满足:对于圆
),满足:对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为同一常数,试求所有满足条件的点
为同一常数,试求所有满足条件的点![]() 的坐标及该常数.
的坐标及该常数.
【答案】![]()
![]() ;
;![]() 在直线
在直线![]() 上存在定点
上存在定点![]() 使得
使得![]() 为常数
为常数![]() .
.
【解析】
![]() 化简圆的方程为标准方程,求出圆的半径,转化求解实数
化简圆的方程为标准方程,求出圆的半径,转化求解实数![]() 的值;
的值;
![]() 设直线
设直线![]() 上的点
上的点![]() ,取直线
,取直线![]() 与圆
与圆![]() 的交点
的交点![]() ,则
,则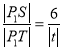 ,
,
取直线![]() 与圆
与圆![]() 的交点
的交点![]() ,则
,则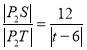 ,然后求解存在这样的定点
,然后求解存在这样的定点![]() ,进而求证结论.
,进而求证结论.
解:![]() 依题意,圆C方程变形为
依题意,圆C方程变形为![]() ,圆心
,圆心![]() ,半径
,半径![]()
又直线l的方程即为![]()
因为![]() 垂直平分弦
垂直平分弦![]() ,
,![]() 圆心
圆心![]() 必在直线
必在直线![]() 上
上
![]()
![]() 过点
过点![]() 和
和![]() ,斜率
,斜率![]() ,
,![]()
![]()
![]() 设直线
设直线![]() 上的点
上的点![]() 取直线
取直线![]() 与圆
与圆![]() 的交点
的交点![]() ,则
,则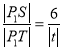
取直线![]() 与圆
与圆![]() 的交点
的交点![]() ,则
,则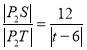 .
.
令![]() ,解得
,解得![]() 或
或![]() (舍去,与
(舍去,与![]() 重合),此时
重合),此时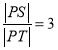
若存在这样的定点![]() 满足题意,则必为
满足题意,则必为![]()
下证:点![]() 满足题意.设圆上任意一点
满足题意.设圆上任意一点![]() ,则
,则![]()
![]()
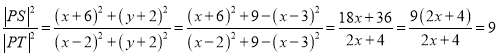
![]()
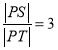
综上可知,在直线![]() 上存在定点
上存在定点![]() 使得
使得![]() 为常数
为常数![]() .
.

练习册系列答案
相关题目
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
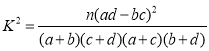 ,其中
,其中![]() .
.

