题目内容
2.过l1:2x-3y+2=0与l2:3x-4y+2=0的交点且与直线4x+y-4=0平行的直线方程为4x+y-10=0.分析 联立方程,解方程组可得直线交点,由平行关系可设直线的方程为4x+y+c=0,代点可得c值,可得直线方程.
解答 解:联立$\left\{\begin{array}{l}{2x-3y+2=0}\\{3x-4y+2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
由平行关系可设所求直线的方程为4x+y+c=0,
代点(2,2)可得c=-10,
∴直线的方程为:4x+y-10=0.
点评 本题考查直线的一般式方程和平行关系,属基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
14.下列赋值语句中正确的是( )
| A. | 4=n | B. | n=n+1 | C. | n+1=m | D. | m+n=0 |
11.已知P是直线;“3x+4y+13=0的动点,PA是圆C:x2+y2-2x-2y-2=0的一条切线,A是切点,那么△PAC的面积的最小值是( )
| A. | 5$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
12.在数列{an}中,a1=1且已知an+1=2an-3,则a4等于( )
| A. | 5 | B. | -5 | C. | -13 | D. | -29 |
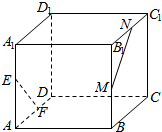 已知点E,F,M,N分别为正方体ABCD-A1B1C1D1的棱AA1,AD,BB1,B1C1的中点,则异面直线EF和MN所成的角为90°.
已知点E,F,M,N分别为正方体ABCD-A1B1C1D1的棱AA1,AD,BB1,B1C1的中点,则异面直线EF和MN所成的角为90°.