题目内容

等差数列{an}中，Sn=n2，则a17+a18+a19+a20的值为
 
．
考点：等差数列的性质
专题：等差数列与等比数列
分析：可得a17+a18+a19+a20=S20-S16，由已知式子代值可得答案．
解答： 解：∵在等差数列{an}中，Sn=n2，
∴a17+a18+a19+a20=S20-S16
=202-162=144
故答案为：144
点评：本题考查等差数列的片段和，属基础题．
练习册系列答案
相关题目
数列{an}满足：na1+（n-1）a2+…+2an-1+an=（
9
10
）n-1+（
9
10
）n-2+…+
9
10
+1（n=1，2，3…）
（1）求a1，a2，a3的值；
（2）求an的通项公式；
（3）若bn=-（n+1）an，试问是否存在正整数k，使得对于任意的正整数n，都有bn≤bk成立？若存在求出k的值，若不存在请说明理由．
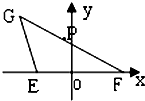已知E、F是x轴上的点，坐标原点O为线段EF的中点，G、P是坐标平面上的动点，点P在线段FG上，|
FG
|=10，|
EF
|=6，（
PE
+
1
2
EG
）•
EG
=0．
（1）求P的轨迹C的方程；
（2）A、B为轨迹C上任意两点，且
OE
=α
OA
+（1-α）
OB
，M为AB的中点，求△OEM面积的最大值．
已知二次函数y=f（x的）顶点坐标为（-
3
2
，49），且f（x）=0的两个实根之差等于7，f（x）=
 
．
已知函数f（x）=
(1-a2)x2+3(1-a)x+6
，若f（x）定义域为R，则实数a的取值范围
 
．
已知圆O1和圆O2的极坐标方程分别为ρ2-2
2
ρcos（θ-
π
4
）=2，ρ=2．则经过两圆交点的直线的极坐标方程为
 
．
巳知等比数列{an}满足a＞0，n∈N*，且a5•a2n-5=22n（n≥3），则当n≥3时，an=
 
．
有五名男教师，4名女教师，现从中选派3名男教师和2名女教师分别到五个乡村支教，不同的选派方法有
 
种．
已知数列{an}的前4项分别为1，
1
3
，
1
6
，
1
10
，猜想数列{an}的一个通项公式为an=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网