题目内容
如图所示,流程图给出了无穷等差整数列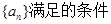 ,
,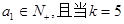 时,输出的
时,输出的 时,输出的
时,输出的 (其中d为公差)
(其中d为公差)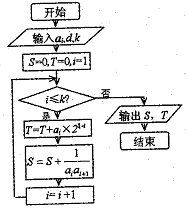
(I)求数列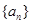 的通项公式;
的通项公式;
(II)是否存在最小的正数m,使得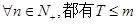 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。
(I) (II)
(II)
解析试题分析:(1)根据框图
所以有
解得
(2)事实上, ,利用错位相消得
,利用错位相消得
考点:数列与不等式的综合;等差数列的通项公式;数列的求和;循环结构.
点评:本题考查数列、算法与函数的综合问题,本题解题的关键利用错位相减法求数列的和,再用函数的思想来解题,本题是一个综合题目,难度可以作为高考卷的压轴题.

练习册系列答案
相关题目
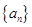 中,
中,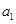 、
、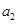 、
、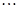 、
、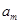 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列, 、
、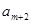 、
、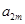 ,构成首项为
,构成首项为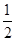 ,公比为
,公比为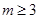 ,
,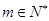 .
.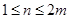 ,
,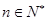 ,都有
,都有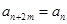 成立.
成立.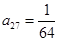 时,求
时,求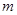 的值;
的值;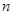 项和为
项和为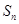 .判断是否存在
.判断是否存在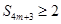 成立?若存在,求出
成立?若存在,求出 的公差为
的公差为 ,且
,且 成等比数列.
成等比数列. ,求数列
,求数列 的前
的前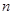 项和
项和 .
.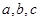 ,求证:
,求证: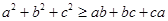 ;
;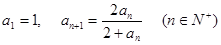 ,写出
,写出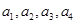 并猜想这个数列的通项公式达式.
并猜想这个数列的通项公式达式.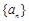 是等比数列,
是等比数列,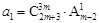 ,公比
,公比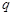 是
是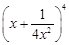 的展开式中的第二项(按x的降幂排列).
的展开式中的第二项(按x的降幂排列).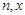 表示通项
表示通项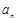 与前n项和
与前n项和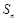 ;
;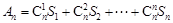 ,用
,用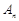 .
.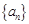 的各项都是正数,前
的各项都是正数,前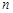 项和为
项和为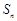 ,且对任意
,且对任意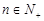 ,都有
,都有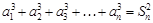 .
.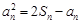 ; (2)求数列
; (2)求数列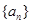 的前
的前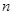 项和
项和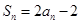 .数列
.数列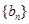 满足:
满足: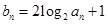 .
.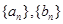 的通项
的通项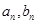 .并比较
.并比较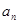 与
与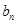 的大小;
的大小;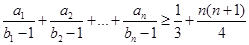 .
.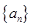 的前
的前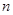 项和
项和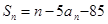 ,
,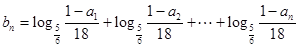 ,求数列
,求数列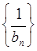 的前
的前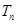 .
.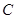 :
: ,数列
,数列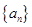 的首项
的首项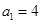 ,且
,且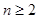 时,点
时,点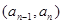 恒在曲线
恒在曲线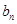 }满足
}满足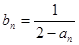
 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;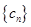 满足
满足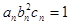 ,试比较数列
,试比较数列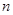 项和
项和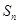 与
与 的大小.
的大小.