题目内容
已知曲线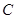 :
: ,数列
,数列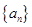 的首项
的首项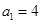 ,且
,且
当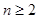 时,点
时,点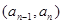 恒在曲线
恒在曲线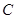 上,数列{
上,数列{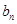 }满足
}满足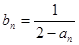
(1)试判断数列 是否是等差数列?并说明理由;
是否是等差数列?并说明理由;
(2)求数列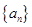 和
和 的通项公式;
的通项公式;
(3)设数列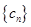 满足
满足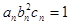 ,试比较数列
,试比较数列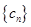 的前
的前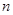 项和
项和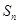 与
与 的大小.
的大小.
(1)数列{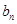 }是公差为
}是公差为 的等差数列
的等差数列
(2)  ,
,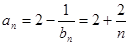
(3)根据通项公式的特点,采用裂项法来求和,并能比较大小。
解析试题分析:解;(1)∵当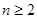 时,点
时,点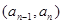 恒在曲线C上
恒在曲线C上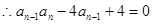 1分
1分
由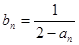 得
得
当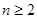 时,
时,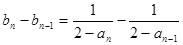
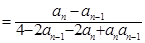
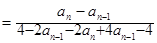
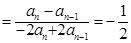 5分
5分
∴数列{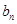 }是公差为
}是公差为 的等差数列. 6分
的等差数列. 6分
(2)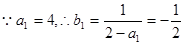
 8分
8分
由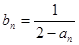 得
得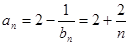 10分
10分
(3)
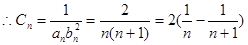 12分
12分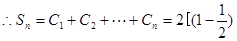
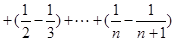 ]
]
14分
考点:等差数列,等比数列
点评:解决的关键是利用数列的概念以及裂项法求和进而比较大小,属于基础题。

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
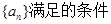 ,
,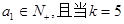 时,输出的
时,输出的 时,输出的
时,输出的 (其中d为公差)
(其中d为公差)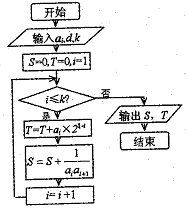
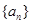 的通项公式;
的通项公式;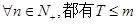 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。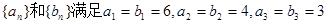 ,且数列
,且数列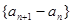 是等差数列,
是等差数列,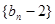 是等比数列.
是等比数列.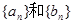 的通项公式;
的通项公式;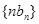 的前
的前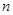 项和为
项和为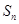 ,求
,求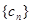 满足
满足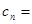
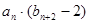 ,求数列
,求数列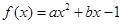 ,且不等式
,且不等式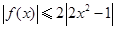 对任意的实数
对任意的实数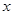 恒成立,数列
恒成立,数列 满足
满足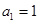 ,
,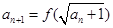
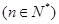 .
. 的值;
的值; .
.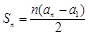 .
.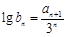 ,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(其中1<p<q),使b1,bp,bq成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.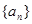 的前
的前 项和为
项和为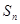 ,且满足
,且满足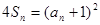 (
(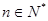 ).
).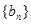 的通项公式为
的通项公式为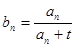 (
(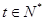 ),若
),若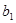 ,
,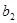 ,
,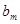 (
(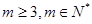 )成等差数列,求
)成等差数列,求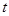 和
和 的值;
的值;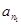 ,
,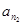 ,
,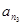 .
.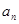 }中,a1=3,
}中,a1=3,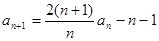 ,
,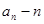 关于n的表达式(不用证明);
关于n的表达式(不用证明);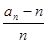 }是什么类型的数列并证明;
}是什么类型的数列并证明; }的前n项和为
}的前n项和为 ,且
,且 =1,
=1,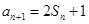 ,数列{
,数列{ }满足
}满足 ,点P(
,点P( )在直线x―y+2=0上,
)在直线x―y+2=0上, .
. ,求数列{
,求数列{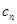 }的前n项和
}的前n项和 .
.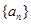 前
前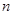 项和
项和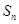 满足
满足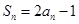 ,等差数列
,等差数列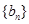 满足
满足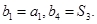
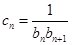 ,数列
,数列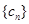 的前
的前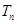 ,问
,问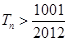 的最小正整数n是多少?
的最小正整数n是多少?