若菱形ABCD的边长为2.则|$\overrightarrow{AB}$-$\overrightarrow{AD}$+$\overrightarrow{CD}$|=( )A．2$\sqrt{3}$B．4C．$\sqrt{3}$D．2 题目和参考答案——青夏教育精英家教网—

题目内容

16．若菱形ABCD的边长为2，则|$\overrightarrow{AB}$-$\overrightarrow{AD}$+$\overrightarrow{CD}$|=（　　）

A．

2$\sqrt{3}$

B．

C．

$\sqrt{3}$

D．

分析利用向量的运算法则将|$\overrightarrow{AB}$-$\overrightarrow{AD}$+$\overrightarrow{CD}$|化简，利用菱形ABCD的边长为2得到向量模的值．

解答解：∵菱形ABCD的边长为2，
∴|$\overrightarrow{AB}$-$\overrightarrow{AD}$+$\overrightarrow{CD}$|=|$\overrightarrow{AB}$+$\overrightarrow{DA}$+$\overrightarrow{CD}$|=|$\overrightarrow{BC}$|=2．
故选：D．

点评本题考查了向量的三角形法则的运用以及向量的模的意义，属于基础题．

练习册系列答案

初中毕业学业考试模拟试卷湖南教育出版社系列答案

畅行课堂系列答案

学习周报系列答案

智能训练练测考系列答案

7．在平面直角坐标系中，A（1，-1），B（1，3），点C在直线x-y+1=0上．
（1）若直线AC的斜率是直线BC的斜率的2倍，求直线AC的方程；
（2）点B关于y轴对称点为D，若以DC为直径的圆M过点A，求C的坐标．

4．

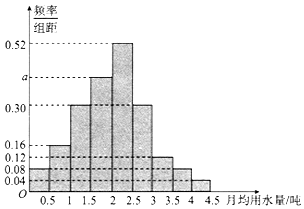我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．
（Ⅰ）求直方图中a的值；
（Ⅱ）若该市有110万居民，估计全市居民中月均用水量不低于3吨的人数，请说明理由；
（Ⅲ）若该市政府希望使80%的居民每月的用水量不超过标准x（吨），估计x的值（精确到0.01），并说明理由．

11．若角α是第四象限角，则角-α的终边在（　　）

1．把函数y=sin（x-$\frac{π}{3}$）的图象向左平移$\frac{π}{6}$个单位长度，再将图象上所有点的横坐标缩短为原来的$\frac{1}{2}$倍（纵坐标不变）得到函数f（x）的图象．
（Ⅰ）写出函数f（x）的解析式；
（Ⅱ）若x∈[0，$\frac{5π}{6}$]时，关于x的方程f（x）-m=0有两个不等的实数根，求实数m的取值范围．

8．若椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上一点P到椭圆一个焦点的距离为4，则P到另一焦点距离为（　　）

1．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，又$\overrightarrow{OC}=2\overrightarrow{a}+\overrightarrow{b}$，$\overrightarrow{OD}=\overrightarrow{a}+3\overrightarrow{b}$．求|$\overrightarrow{CD}$|的值．

2．已知函数f（x）=$\frac{x}{{e}^{x}}$（e是对自然对数的底数），则其导函数f'（x）=（　　）

A．

$\frac{1+x}{{e}^{x}}$

B．

$\frac{1-x}{{e}^{x}}$

试题分类