题目内容
4.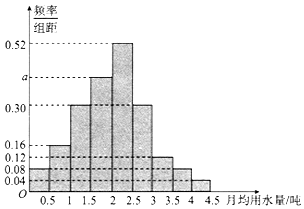 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(Ⅰ)求直方图中a的值;
(Ⅱ)若该市有110万居民,估计全市居民中月均用水量不低于3吨的人数,请说明理由;
(Ⅲ)若该市政府希望使80%的居民每月的用水量不超过标准x(吨),估计x的值(精确到0.01),并说明理由.
分析 (Ⅰ)由概率统计相关知识,各组频率和为1,列出方程求出a的值;
(Ⅱ)由图计算不低于3吨的频率和频数即可;
(Ⅲ)由图计算月均用水量小于2.5吨的频率和月均用水量小于3吨的频率,
假设月均用水量平均分布,由此求出x的值.
解答 解:(Ⅰ)由概率统计相关知识,各组频率和为1,
即0.5×(0.08+0.16+0.3+a+0.52+0.3+0.12+0.08+0.04)=1,
解得a=0.4;…(3分)
(Ⅱ)由图知,不低于3吨的人数所占比例为
0.5×(0.12+0.08+0.04)=0.12,
∴全市月均用水量不低于3吨的人数为
110×0.12=13.2(万);…(7分)
(Ⅲ)由图可知,月均用水量小于2.5吨的居民人数所占比例为
0.5×(0.08+0.16+0.3+0.4+0.52)=0.73,…(9分)
即73%的居民月均用水量小于2.5吨;
同理,88%的居民月均用水量小于3吨,故2.5<x<3;
假设月均用水量平均分布,则
$x=2.5+0.5×\frac{(0.8-0.73)÷0.5}{0.3}≈2.73$(吨).…(12分)
点评 本题考查了利用频率分布直方图求频率、频数的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列有关命题的说法中,正确的是( )
| A. | 命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” | |
| B. | 命题“若α>β,则sinα>sinβ”的逆否命题为真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,都有x2+x+1>0” | |
| D. | “x>1”是“x2+x-2>0”的充分不必要条件 |
16.若菱形ABCD的边长为2,则|$\overrightarrow{AB}$-$\overrightarrow{AD}$+$\overrightarrow{CD}$|=( )
| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |
 在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.
在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(-1,0),离心率e=$\frac{{\sqrt{2}}}{2}$.