题目内容
13.在△ABC中,求证:S△ABC=$\frac{{a}^{2}}{2(cotB+cotC)}$.分析 由三角形面积公式可得S△ABC=$\frac{1}{2}$absinC,且由正弦定理可得:sinB=$\frac{b}{2R}$,sinA=$\frac{a}{2R}$,利用同角三角函数基本关系式,两角和的正弦函数公式,正弦定理,化简等式右边可证等于左边,从而得证.
解答 解:∵S△ABC=$\frac{1}{2}$absinC,且由正弦定理可得:sinB=$\frac{b}{2R}$,sinA=$\frac{a}{2R}$,
∴$\frac{{a}^{2}}{2(cotB+cotC)}$=$\frac{{a}^{2}}{2(\frac{cosB}{sinB}+\frac{cosC}{sinC})}$=$\frac{{a}^{2}}{2\frac{cosBsinC+cosCsinB}{sinBsinC}}$=$\frac{{a}^{2}}{2\frac{sinA}{sinBsinC}}$=$\frac{{a}^{2}sinBsinC}{2sinA}$=$\frac{{a}^{2}×\frac{b}{2R}×sinC}{2×\frac{a}{2R}}$=$\frac{1}{2}$absinC=S△ABC.
得证.
点评 本题主要考查了同角三角函数基本关系式,两角和的正弦函数公式,正弦定理,三角形面积公式在解三角形中的应用,属于中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
8.一个物体的运动方程是s=3tcost+x(x为常数),则其速度方程为( )
| A. | v=3cost-3tsint+1 | B. | v=3cost-3tsint | ||
| C. | v=-3sint | D. | v=3cost+3tsint |
18.已知集合A={x|x2-3x+2>0},集合B={y|y=2cosx+1},则(∁RA)∩B=( )
| A. | (-∞,-1)∪(2,+∞) | B. | [1,2] | C. | [-1,1)∪(2,3] | D. | [-1,3] |
5.已知函数f(x)=$\frac{x}{x+1}$+2x-mln(x+1)在(0,+∞)上是增函数,则实数m的取值范围为( )
| A. | (-∞,2$\sqrt{2}$] | B. | (-∞,2$\sqrt{2}$) | C. | (-∞,3) | D. | (-∞,3] |
2.设函数f(x)=|2x-1|,c<b<a,且f(c)>f(a)>f(b),则下列关系式正确的是( )
| A. | a+c≤0 | B. | a+c>0 | C. | a+c≤0 | D. | a+c<0 |
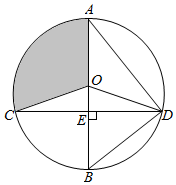 如图,已知⊙O的直径AB垂直于弦CD于E,连结 AD、BD、OC、OD,且 OD=5.
如图,已知⊙O的直径AB垂直于弦CD于E,连结 AD、BD、OC、OD,且 OD=5.