题目内容
20．若直线x-y=2被圆（x-a）2+y2=4所截得的弦长为2$\sqrt{2}$，则正数a=（ ）| A． | 4或0 | B． | 4 | C． | $\sqrt{3}$ | D． | 0 |
分析 由已知得圆心（a，0）到直线x-y=2的距离d=$\sqrt{4-2}$=$\sqrt{2}$，由此利用点到直线的距离公式能求出实数a的值．
解答 解：∵直线x-y=2被圆（x-a）2+y2=4所截得的弦长为2$\sqrt{2}$，
∴圆心（a，0）到直线x-y=2的距离d=$\sqrt{4-2}$=$\sqrt{2}$，
∴d=$\frac{|a-2|}{\sqrt{2}}$=$\sqrt{2}$，
解得a=0或a=4，
∵a＞0，∴a=4，
故选B．
点评 本题考查实数值的求法，是基础题，解题时要注意圆的性质和点到直线的距离公式的合理运用．
练习册系列答案
相关题目
10．一个四棱锥的三视图如图所示，这个四棱锥的体积为（ ）
| A． | 6 | B． | 8 | C． | 12 | D． | 24 |
11．手机完全充满电量，在开机不使用的状态下，电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间．为了解A，B两个不同型号手机的待机时间，现从某卖场库存手机中随机抽取A，B两个型号的手机各5台，在相同条件下进行测试，统计结果如下：
已知 A，B两个型号被测试手机待机时间的平均值相等．
（Ⅰ）求a的值；
（Ⅱ）判断A，B两个型号被测试手机待机时间方差的大小（结论不要求证明）；
（Ⅲ）从被测试的手机中随机抽取A，B型号手机各1台，求至少有1台的待机时间超过122小时的概率．
（注：n个数据x1，x2，…，xn的方差s2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]，其中$\overline{x}$为数据x1，x2，…，xn的平均数）
| 手机编号 | 1 | 2 | 3 | 4 | 5 |
| A型待机时间（h） | 120 | 125 | 122 | 124 | 124 |
| B型待机时间（h） | 118 | 123 | 127 | 120 | a |
（Ⅰ）求a的值；
（Ⅱ）判断A，B两个型号被测试手机待机时间方差的大小（结论不要求证明）；
（Ⅲ）从被测试的手机中随机抽取A，B型号手机各1台，求至少有1台的待机时间超过122小时的概率．
（注：n个数据x1，x2，…，xn的方差s2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]，其中$\overline{x}$为数据x1，x2，…，xn的平均数）
15．
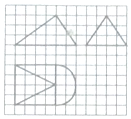如图，网格纸上校正方形的边长为1，粗线画出的某几何体的三视图，其中俯视图的右边为一个半圆，则此几何体的体积为（ ）
如图，网格纸上校正方形的边长为1，粗线画出的某几何体的三视图，其中俯视图的右边为一个半圆，则此几何体的体积为（ ）| A． | 16+4π | B． | 16+2π | C． | 48+4π | D． | 48+2π |
5．设函数f（x）=cosx+2sinx，则f′（$\frac{π}{4}$）=（ ）
| A． | -$\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{2}$ | D． | -$\sqrt{2}$ |