题目内容
10.一个四棱锥的三视图如图所示,这个四棱锥的体积为( )
| A. | 6 | B. | 8 | C. | 12 | D. | 24 |
分析 几何体是四棱锥,再根据三视图判断四棱锥的高与底面长方形的长与宽,把数据代入棱锥的体积计算可得答案.
解答 解:由三视图知几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,高为2,
四棱锥的底面是长方形,长方形的长、宽分别为4、3,
∴几何体的体积V=$\frac{1}{3}$×3×4×2=8.
故选:B.
点评 本题考查了由三视图求几何体的体积,解题的关键是判断几何体的形状及数据所对应的几何量.

练习册系列答案
相关题目
20.已知曲线$f(x)=lnx+\frac{x^2}{a}$在点(1,f(1))处的切线的倾斜角为$\frac{3π}{4}$,则a的值为( )
| A. | 1 | B. | -4 | C. | $-\frac{1}{2}$ | D. | -1 |
1.甲袋中有16个白球和17个黑球,乙袋中有31个白球,现每次任意从甲袋中摸出两个球,如果两球同色,则将这两球放进丙袋,并从乙袋中拿出一白球放回甲袋;如果两球不同色,则将白球放进丙袋,并把黑球放回甲袋.那么这样拿 次后,甲袋中只剩一个球,这个球的颜色是 ( )
| A. | 16,黑色 | B. | 16,白色或黑色 | C. | 32,黑色 | D. | 32,白色 |
19.已知双曲线以△ABC的顶点B,C为焦点,且经过点A,若△ABC内角的对边分别为a,b,c.且a=4,b=5,$c=\sqrt{21}$,则此双曲线的离心率为( )
| A. | $5-\sqrt{21}$ | B. | $\frac{{\sqrt{21}+5}}{2}$ | C. | $5+\sqrt{21}$ | D. | $\frac{{5-\sqrt{21}}}{2}$ |
20.若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2$\sqrt{2}$,则正数a=( )
| A. | 4或0 | B. | 4 | C. | $\sqrt{3}$ | D. | 0 |
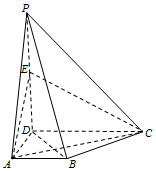 如图,在四棱锥P-ABCD 中,PD⊥底面ABCD,AB∥DC,CD=2AB,AD⊥CD,E为棱PD的中点.
如图,在四棱锥P-ABCD 中,PD⊥底面ABCD,AB∥DC,CD=2AB,AD⊥CD,E为棱PD的中点.