题目内容
(本小题满分12分)
已知椭圆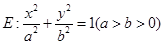 过点
过点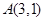 ,左、右焦点分别为
,左、右焦点分别为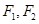 ,离心率为
,离心率为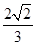 ,经过
,经过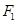 的直线
的直线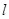 与圆心在
与圆心在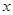 轴上且经过点
轴上且经过点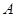 的圆
的圆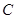 恰好相切于点
恰好相切于点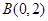 .
.
(1)求椭圆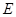 及圆
及圆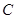 的方程;
的方程;
(2) 在直线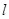 上是否存在一点
上是否存在一点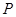 ,使
,使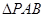 为以
为以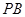 为底边的等腰三角形?若存在,求点
为底边的等腰三角形?若存在,求点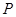 的坐标,否则说明理由.
的坐标,否则说明理由.
已知椭圆
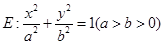 过点
过点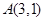 ,左、右焦点分别为
,左、右焦点分别为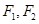 ,离心率为
,离心率为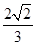 ,经过
,经过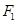 的直线
的直线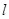 与圆心在
与圆心在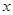 轴上且经过点
轴上且经过点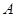 的圆
的圆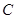 恰好相切于点
恰好相切于点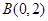 .
.(1)求椭圆
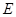 及圆
及圆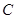 的方程;
的方程;(2) 在直线
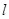 上是否存在一点
上是否存在一点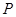 ,使
,使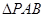 为以
为以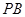 为底边的等腰三角形?若存在,求点
为底边的等腰三角形?若存在,求点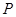 的坐标,否则说明理由.
的坐标,否则说明理由.解:(1)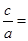
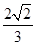 ,则
,则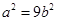 ,
,
∴椭圆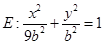 ,
,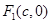 ,
,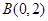
∴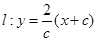 …………3分
…………3分
设圆心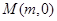 ,半径
,半径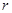 ,则由
,则由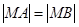 ,得
,得
∴圆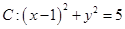 ,又
,又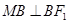
∴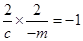 ,从而
,从而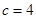 ,结合
,结合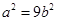 得
得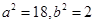
∴椭圆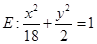 ………………………6分
………………………6分
(2)假设存在一点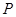 ,使
,使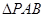 为以
为以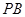 为底边的等腰三角形,则有
为底边的等腰三角形,则有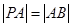 ,
,
由(1)知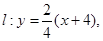 即
即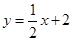 ,设直线
,设直线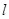 上的点
上的点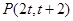 ,
,
∴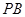 中点
中点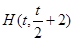 ,又
,又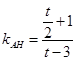 ,
,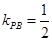 ,
,
由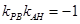 得
得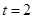
∴所求的点为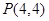 ……………………………12分
……………………………12分
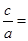
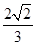 ,则
,则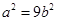 ,
,∴椭圆
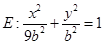 ,
,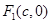 ,
,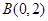
∴
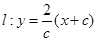 …………3分
…………3分设圆心
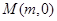 ,半径
,半径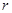 ,则由
,则由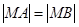 ,得
,得
∴圆
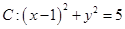 ,又
,又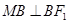
∴
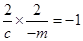 ,从而
,从而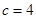 ,结合
,结合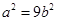 得
得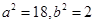
∴椭圆
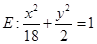 ………………………6分
………………………6分(2)假设存在一点
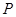 ,使
,使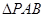 为以
为以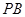 为底边的等腰三角形,则有
为底边的等腰三角形,则有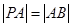 ,
,由(1)知
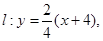 即
即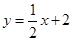 ,设直线
,设直线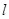 上的点
上的点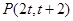 ,
,∴
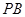 中点
中点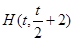 ,又
,又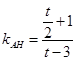 ,
,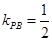 ,
,由
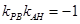 得
得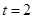
∴所求的点为
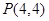 ……………………………12分
……………………………12分略

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
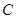 :
: 上有两个相异的点到直线
上有两个相异的点到直线 的距离为都为
的距离为都为 ,则
,则


 .
. 上.则圆的方程为( )
上.则圆的方程为( )



 是圆
是圆 的切线,切点为
的切线,切点为 ,直线
,直线 交圆
交圆 两点,
两点,  ,
, ,则切线PA的长度等于 .
,则切线PA的长度等于 .
 是圆的内接四边形,
是圆的内接四边形, ,过
,过 点的圆的切线与
点的圆的切线与 的延长线交于
的延长线交于 点,证明:
点,证明: ;
; .
.
 ,
, 为直径的圆C的方程为 ▲ ;
为直径的圆C的方程为 ▲ ;  上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点.
上一点A(4,6)作圆的一条动弦AB,点P为弦AB的中点. 的对称点为E,关于
的对称点为E,关于 的对称点为F,求|EF|的取值范围.
的对称点为F,求|EF|的取值范围.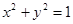 上运动,它与定点B(3,0)连线的中点的轨迹方程式( )
上运动,它与定点B(3,0)连线的中点的轨迹方程式( )