题目内容
15.已知实数x.y满足x2+y2-2x+2$\sqrt{3}$y=0,若总有x+$\sqrt{3}$y+m≥0,则实数m的最小值为6.分析 设直线x+$\sqrt{3}$y=t,圆心到直线的距离d=$\frac{|1-3-t|}{2}$≤2,求出t的范围,总有x+$\sqrt{3}$y+m≥0即,m≥-t,即可得到m的最小值.
解答 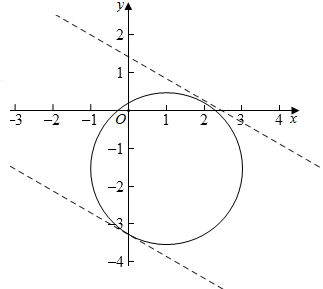 解:∵x2+y2-2x+2$\sqrt{3}$y=0,
解:∵x2+y2-2x+2$\sqrt{3}$y=0,
∴(x-1)2+(y+$\sqrt{3}$)2=4,
设直线x+$\sqrt{3}$y=t,
∴圆心到直线的距离d=$\frac{|1-3-t|}{2}$≤2,
解得-6≤t≤2,
∵x+$\sqrt{3}$y+m≥0,
∴x+$\sqrt{3}$y≥-m,
∴t≥-m,
即m≥-t,
∵-2≤-t≤6,
故实数m的最小值为6,
故答案为:6.
点评 本题考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
16.若f(x)=x2+2x-3,则f(x)在区间[-2,1]上的值域是( )
| A. | [-4,-3] | B. | [-3,0] | C. | [-4,0] | D. | [0,2] |