题目内容
(本小题满分13分)在平面直角坐标系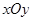 中,已知椭圆
中,已知椭圆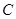 :
: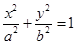 (
(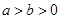 )的左焦点为
)的左焦点为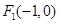 ,且点
,且点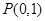 在
在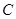 上.
上.
(Ⅰ)求椭圆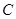 的方程;
的方程;
(Ⅱ)已知直线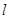 的斜率为2且经过椭圆
的斜率为2且经过椭圆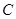 的左焦点.求直线
的左焦点.求直线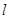 与该椭圆
与该椭圆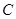 相交的弦长。
相交的弦长。
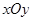 中,已知椭圆
中,已知椭圆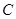 :
: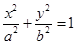 (
(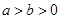 )的左焦点为
)的左焦点为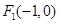 ,且点
,且点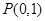 在
在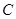 上.
上.(Ⅰ)求椭圆
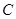 的方程;
的方程;(Ⅱ)已知直线
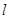 的斜率为2且经过椭圆
的斜率为2且经过椭圆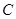 的左焦点.求直线
的左焦点.求直线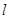 与该椭圆
与该椭圆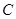 相交的弦长。
相交的弦长。(Ⅰ) .(Ⅱ)
.(Ⅱ)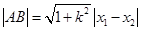 =
=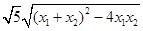 =
=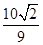 。
。
 .(Ⅱ)
.(Ⅱ)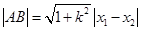 =
=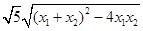 =
=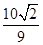 。
。试题分析:(1)根据椭圆的性质可知焦点坐标得到c的值,然后结合点在椭圆上得到a,b的关系式,进而求解椭圆方程。(2)根据题意设出直线方程,那么与椭圆联立方程组,结合韦达定理得到弦长公式。
(Ⅰ)因为椭圆
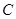 的左焦点为
的左焦点为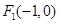 ,所以
,所以 ,
,点
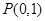 代入椭圆
代入椭圆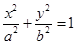 ,得
,得 ,即
,即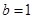 ,
,所以
 ,所以椭圆
,所以椭圆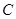 的方程为
的方程为 .
.(Ⅱ)直线
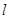 的方程为
的方程为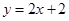 ,
, ,消去
,消去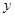 并整理得
并整理得 ,
, ,
,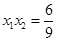
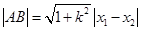 =
=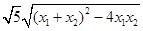 =
=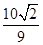 ,
,点评:解决该试题的关键是能够熟练的利用a,b,c的关系式,求解椭圆的方程,以及能运用设而不求的思想,设点,接和韦达定理表示出弦长公式。

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
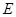 :
: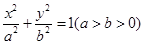 的左焦点为
的左焦点为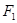 ,右焦点为
,右焦点为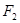 ,离心率
,离心率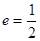 .过
.过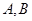 两点,且△
两点,且△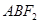 的周长为
的周长为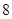 .
.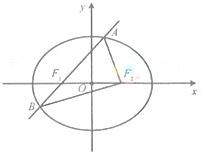
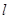 :
: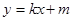 与椭圆
与椭圆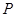 ,且与直线
,且与直线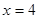 相交于点
相交于点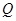 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点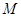 ,使得以
,使得以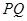 为直径的圆恒过点
为直径的圆恒过点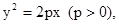 过焦点
过焦点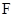 的动直线l交抛物线于A,B两点,O为坐标原点, 求证:
的动直线l交抛物线于A,B两点,O为坐标原点, 求证:  为定值;
为定值;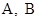 两点, 存在定点
两点, 存在定点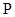 , 使得
, 使得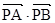 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明. +
+ =1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d.
=1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d. ,求k的值;
,求k的值; ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.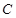 :
: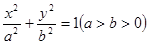 的左、右顶点分别
的左、右顶点分别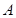 、
、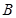 ,椭圆过点
,椭圆过点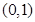 且离心率
且离心率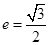 .
.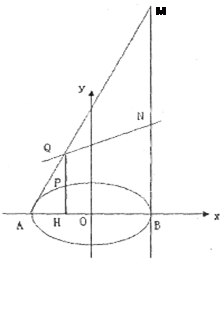
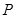 作
作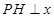 轴,
轴,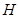 为垂足,延长
为垂足,延长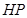 到点
到点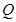 ,且
,且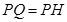 ,过点
,过点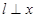 轴,连结
轴,连结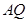 并延长交直线
并延长交直线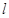 于点
于点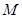 ,线段
,线段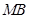 的中点记为点
的中点记为点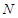 .
.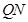 与以
与以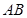 为直径的圆
为直径的圆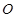 的位置关系, 并证明.
的位置关系, 并证明.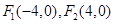 ,动点
,动点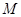 满足条件:
满足条件: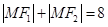 ,则点
,则点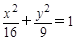
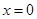
 (
(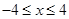 )
)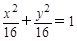
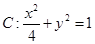 ,左右焦点分别为
,左右焦点分别为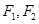 ,
,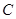 上一点
上一点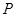 满足
满足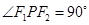 ,求
,求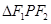 的面积;
的面积;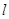 交
交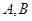 ,线段
,线段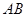 的中点为
的中点为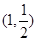 ,求直线
,求直线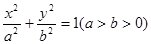 的左、右焦点,A和B是以O(O为坐标原点)为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
的左、右焦点,A和B是以O(O为坐标原点)为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )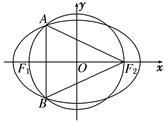


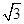 -1
-1 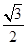

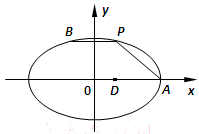
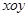 中,已知点
中,已知点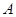 为椭圆
为椭圆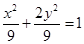 的右顶点, 点
的右顶点, 点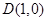 ,点
,点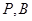 在椭
在椭 .
.
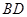 的方程;
的方程;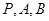 三点的圆
三点的圆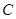 截得的弦长;
截得的弦长; 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.