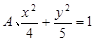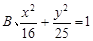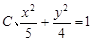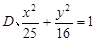题目内容
(本小题满分16分)
椭圆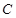 :
: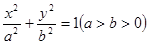 的左、右顶点分别
的左、右顶点分别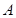 、
、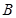 ,椭圆过点
,椭圆过点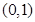 且离心率
且离心率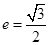 .
.
(1)求椭圆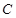 的标准方程;
的标准方程;
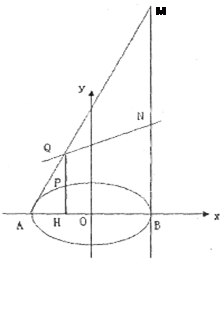
(2)过椭圆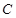 上异于
上异于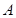 、
、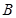 两点的任意一点
两点的任意一点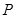 作
作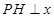 轴,
轴,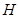 为垂足,延长
为垂足,延长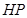 到点
到点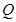 ,且
,且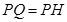 ,过点
,过点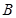 作直线
作直线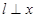 轴,连结
轴,连结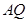 并延长交直线
并延长交直线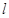 于点
于点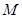 ,线段
,线段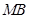 的中点记为点
的中点记为点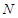 .
.
①求点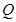 所在曲线的方程;
所在曲线的方程;
②试判断直线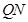 与以
与以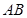 为直径的圆
为直径的圆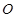 的位置关系, 并证明.
的位置关系, 并证明.
椭圆
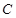 :
: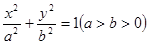 的左、右顶点分别
的左、右顶点分别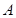 、
、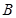 ,椭圆过点
,椭圆过点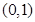 且离心率
且离心率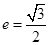 .
.
(1)求椭圆
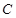 的标准方程;
的标准方程;(2)过椭圆
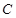 上异于
上异于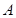 、
、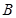 两点的任意一点
两点的任意一点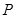 作
作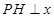 轴,
轴,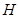 为垂足,延长
为垂足,延长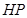 到点
到点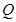 ,且
,且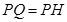 ,过点
,过点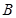 作直线
作直线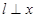 轴,连结
轴,连结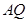 并延长交直线
并延长交直线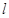 于点
于点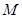 ,线段
,线段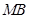 的中点记为点
的中点记为点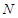 .
.①求点
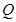 所在曲线的方程;
所在曲线的方程;②试判断直线
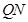 与以
与以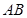 为直径的圆
为直径的圆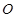 的位置关系, 并证明.
的位置关系, 并证明.(1) (2)①
(2)① ②直线与圆相切,证明:AQ的方程为
②直线与圆相切,证明:AQ的方程为 ,
, ,
, ,
, ,
,
 ,
, ∴
∴ ,∴直线QN与圆O相切
,∴直线QN与圆O相切
 (2)①
(2)① ②直线与圆相切,证明:AQ的方程为
②直线与圆相切,证明:AQ的方程为 ,
, ,
, ,
, ,
, ,
, ∴
∴ ,∴直线QN与圆O相切
,∴直线QN与圆O相切试题分析:(1)因为椭圆经过点(0,1),所以
 ,又椭圆的离心率
,又椭圆的离心率 得
得 ,
,即
 ,由
,由 得
得 ,所以
,所以 ,
,故所求椭圆方程为
 。
。(2)①设
 ,则
,则 ,设
,设 ,∵HP=PQ,∴
,∵HP=PQ,∴ 即
即 ,将
,将 代入
代入 得
得 ,
,所以Q点在以O为圆心,2为半径的圆上,即Q点在以AB为直径的圆O上。
②又A(-2,0),直线AQ的方程为
 ,令
,令 ,则
,则 ,
,又B(2,0),N为MB的中点,∴
 ,
, ,
,
∴

 ,∴
,∴ ,∴直线QN与圆O相切。
,∴直线QN与圆O相切。点评:最后一问判断直线与圆的位置关系转化为向量简化了解题

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
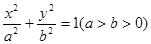 和
和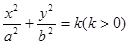 具有 ( )
具有 ( )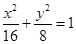 的离心率为( )
的离心率为( )


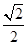
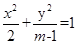 (
( )的曲线C,下列说法错误的是
)的曲线C,下列说法错误的是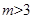 时,曲线C是焦点在y轴上的椭圆
时,曲线C是焦点在y轴上的椭圆 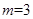 时,曲线C是圆
时,曲线C是圆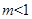 时,曲线C是双曲线
时,曲线C是双曲线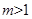 时,曲线C是椭圆
时,曲线C是椭圆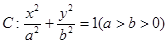 过点
过点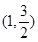 ,且离心率e=
,且离心率e=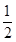 .
.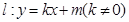 与椭圆交于不同的两点
与椭圆交于不同的两点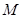 、
、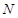 ,且线段
,且线段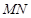 的垂直平分线过定点
的垂直平分线过定点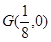 ,求
,求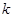 的取值范围。
的取值范围。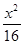 +
+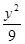 =1的两焦点,经点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )
=1的两焦点,经点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于( )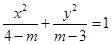 表示焦点在
表示焦点在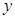 轴上的椭圆,则
轴上的椭圆,则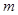 的取值范围是 ( )
的取值范围是 ( )



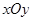 中,已知椭圆
中,已知椭圆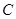 :
: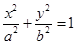 (
(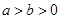 )的左焦点为
)的左焦点为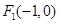 ,且点
,且点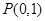 在
在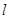 的斜率为2且经过椭圆
的斜率为2且经过椭圆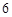 ,离心率
,离心率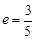 ,焦点在
,焦点在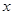 轴上的椭圆标准方程是 ( )
轴上的椭圆标准方程是 ( )