题目内容
(本小题满分14分)如图,椭圆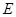 :
: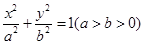 的左焦点为
的左焦点为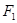 ,右焦点为
,右焦点为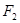 ,离心率
,离心率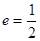 .过
.过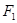 的直线交椭圆于
的直线交椭圆于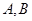 两点,且△
两点,且△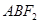 的周长为
的周长为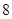 .
.
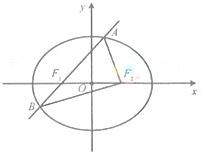
(Ⅰ)求椭圆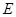 的方程.
的方程.
(Ⅱ)设动直线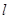 :
: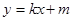 与椭圆
与椭圆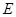 有且只有一个公共点
有且只有一个公共点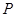 ,且与直线
,且与直线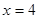 相交于点
相交于点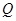 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点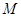 ,使得以
,使得以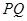 为直径的圆恒过点
为直径的圆恒过点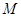 ?若存在,求出点
?若存在,求出点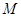 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
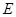 :
: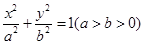 的左焦点为
的左焦点为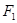 ,右焦点为
,右焦点为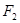 ,离心率
,离心率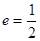 .过
.过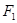 的直线交椭圆于
的直线交椭圆于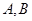 两点,且△
两点,且△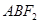 的周长为
的周长为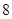 .
.
(Ⅰ)求椭圆
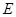 的方程.
的方程.(Ⅱ)设动直线
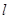 :
: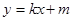 与椭圆
与椭圆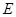 有且只有一个公共点
有且只有一个公共点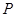 ,且与直线
,且与直线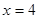 相交于点
相交于点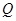 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点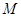 ,使得以
,使得以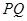 为直径的圆恒过点
为直径的圆恒过点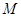 ?若存在,求出点
?若存在,求出点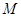 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.(Ⅰ) ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
 ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.试题分析:(Ⅰ)∵过
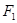 的直线交椭圆于
的直线交椭圆于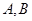 两点,且△
两点,且△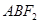 的周长为
的周长为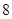 .
.∴
 ∴
∴ ∵
∵ ,∴
,∴ ,∴
,∴
∴椭圆
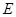 的方程为
的方程为 ……4分
……4分(Ⅱ)由
 ,消元可得:
,消元可得: ……5分
……5分∵动直线
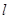 :
: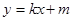 与椭圆
与椭圆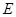 有且只有一个公共点
有且只有一个公共点 ,
,∴
 ∴
∴ ∴
∴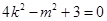 ,
, 此时
 即
即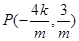 ,
,由
 得
得 ……8分
……8分取
 ,此时
,此时 ,
,以
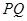 为直径的圆为
为直径的圆为 ,交
,交 轴于点
轴于点 ,
,取
 ,此时
,此时 ,
,以
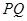 为直径的圆为
为直径的圆为 交
交 轴于点
轴于点 或
或 ,
,故若满足条件的点
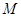 存在,即
存在,即 , ……12分
, ……12分证明如下
∵
 ,
,∴
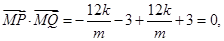
故以
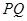 为直径的圆恒过
为直径的圆恒过 轴上的定点
轴上的定点 . ……14分
. ……14分点评:遇到直线与椭圆的位置关系的题目,往往免不了要把直线方程和椭圆方程联立方程组,消去一个未知数,然后利用根与系数的关系进行解答,有时也和向量结合起来解决问题,运算量比较大,难度中等偏上,但是是高考中常考的题目,必须加以重视.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
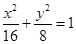 的离心率为( )
的离心率为( )


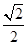
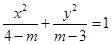 表示焦点在
表示焦点在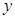 轴上的椭圆,则
轴上的椭圆,则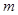 的取值范围是 ( )
的取值范围是 ( )



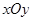 中,已知椭圆
中,已知椭圆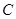 :
: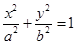 (
(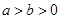 )的左焦点为
)的左焦点为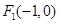 ,且点
,且点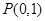 在
在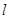 的斜率为2且经过椭圆
的斜率为2且经过椭圆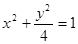 的离心率为( )
的离心率为( )


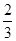
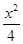 +
+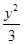 =1的右焦点到直线y=
=1的右焦点到直线y=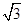 x的距离是 ( )
x的距离是 ( )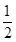
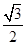
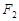 为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,
为圆心作一个圆,使此圆过椭圆中心并交椭圆于点M,N,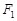 的直线MF1是圆
的直线MF1是圆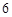 ,离心率
,离心率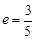 ,焦点在
,焦点在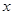 轴上的椭圆标准方程是 ( )
轴上的椭圆标准方程是 ( )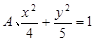
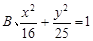
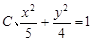
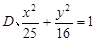
 +
+ =1的离心率 e =
=1的离心率 e = , 则k的值是
, 则k的值是