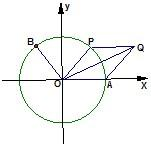
题目内容

如图，A是单位圆与x轴正半轴的交点，点B，P在单位圆上，且B（-
3
5
，
4
5
），∠AOB=α，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
．四边形OAQP的面积为S，
（1）求tan（α-
π
4
）；
（2）求
OQ
•
OA
+S的最大值及此时θ的值．
分析：（1）利用两角差的正切公式进行计算即可．
（2）利用数量积的定义，结合三角函数的图象和性质计算即可．
解答：解：（1）∵B（-
3
5
，
4
5
），∠AOB=α，∴tanα=-
4
3
，
∴tan（α-
π
4
）=
tanα-tan
π
4
1+tanα•tan
π
4
=
-
4
3
-1
1-
4
3
=7．
（2）由已知A（1，0），P（cosθ，sinθ），
则
OQ
=(1+cos?θ，sin?θ)，
OA
?
OQ
=1+cos?θ，
又∵S=sinθ，
∴
OQ
•
OA
+S=sinθ+cosθ+1=
2
sin(θ+
π
4
)+1，（0＜θ＜π）．
∵0＜θ＜π，∴
π
4
＜θ＜
5π
4
，
∴当θ+
π
4
=
π
2
，即θ=
π
4
时，
OQ
•
OA
+S取得最大值1+
2
．
点评：本题主要考查平面向量数量积的应用以及两角和差的正切公式，以及向量和三角函数的综合问题，考查学生的运算能力．
练习册系列答案
相关题目
精英家教网如图，A是单位圆与x轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S．
（1）求
OA
•
OQ
+S的最大值及此时θ的值θ0；
（2）设点B的坐标为(-
3
5
，
4
5
)，∠AOB=α，在（1）的条件下求cos（α+θ0）．
如图，A是单位圆与x轴正半轴的交点，B，P为单位圆上不同的点，∠AOB=θ，∠AOP=2θ，0≤θ≤π．
（Ⅰ）当θ为何值时，
AB
∥
OP
？
（Ⅱ）若
OQ
=
OA
+
OB
，则当θ为何值时，点Q在单位圆上？
（2011•普宁市模拟）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-
3
5
，
4
5
)，∠AOB=α，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S．
（Ⅰ）求cosα+sinα；
（Ⅱ）求
OA
•
OQ
+S的最大值及此时θ的值θ0．
（2012•茂名二模）如图，A是单位圆与x轴正半轴的交点，点B，P在单位圆上，且B（-
3
5
，
4
，5
），∠AOB=α，∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
．设四边形OAQP的面积为S，
（1）求cos（α-
π
6
）；
（2）求f（θ）=
OA
•
OQ
+S的单调递增区间．
（2012•泸州一模）如图，A是单位圆与x轴正半轴的交点，点B、P在单位圆上，且B(-
3
5
，
4
5
)，∠AOB=α．
（Ⅰ）求
4cosα-2sinα
5cosα+3sinα
的值；
（Ⅱ）令∠AOP=θ（0＜θ＜π），
OQ
=
OA
+
OP
，四边形OAQP的面积为S，f(θ)=(
OA
•
OQ
-1)S+S2，求f（θ）的最大值及此时θ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网