题目内容
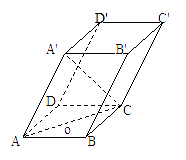 如图,平行六面体ABCD-A'B'C'D'中,AC=2
如图,平行六面体ABCD-A'B'C'D'中,AC=2![]() ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
(1)求侧棱AA'与底面ABCD所成角的大小;
(2)求侧面A'ADD'底面ABCD所成二面角的正切值;
(3)求四棱锥C-A'ADD'的体积.
(1)45°(2)![]() (3)
(3)![]()
解析:
(I)连![]() ,则
,则![]() 平面
平面![]() 于
于![]() ……1分(文1分)
……1分(文1分)
∴![]() 就是侧棱
就是侧棱![]() 与底面
与底面![]() 所成的角 ……1分(文2分)
所成的角 ……1分(文2分)

在![]() 中,
中,![]()
![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
∴![]() ,即侧棱
,即侧棱![]() 与底面
与底面![]() 所成角为45°,
所成角为45°,
(II)在等腰![]() 中,
中,![]() ,∴
,∴![]() ,且O为AC中点,
,且O为AC中点,
过O作![]() 于E,连
于E,连![]() 。∵
。∵![]() 平面ABCD于O,
平面ABCD于O,
由三垂线定理,知![]() ,
,
∴∠![]() 是侧面
是侧面![]() 与底面ABCD所成二面角的平面角。
与底面ABCD所成二面角的平面角。
∵∠ABC=![]() ,
,![]() ,∴底面ABCD是正方形。
,∴底面ABCD是正方形。
∴![]()
![]()
![]() 。
。
在![]() 中,
中,![]() 。
。
即所求二面角的正切值为![]() 。
。
(Ⅲ)由(Ⅱ)知,![]()
![]() 。
。
∴![]() 。
。
∵![]() ,∴
,∴![]() 。
。
∵![]() ,∴平面
,∴平面![]() ,它们的交线是
,它们的交线是![]() 。
。
过O作![]() ,则
,则![]() 。
。
![]() 。
。
又∵![]() 的中点,∴点C到平面
的中点,∴点C到平面![]() 的距离
的距离![]() 。
。
∴![]() 。
。

练习册系列答案
相关题目
 如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为
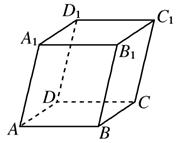
如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为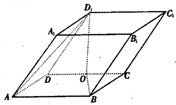 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.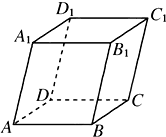 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,