题目内容
10.假设某种产品原来售价为125元/个,厂家打算从元旦至春节期间进行回馈大酬宾活动,每次降价20%.(1)求售价y(元)与降价次数x的函数关系式;
(2)若计划春节期间,产品售价将不低于64元/个,问最多需要降价多少次?
分析 (1)利用指数函数可得结论;
(2)根据计划春节期间,产品售价将不低于64元/个,可得不等式,即可求出最多需要降价的次数.
解答 解:(1)设降价次数为x,则依题意可得y=125×(1-20%)x=125•($\frac{4}{5}$)x,(x∈N) …(4分)
(2)由题意得:125•($\frac{4}{5}$)x≥64…(6分)
即($\frac{4}{5}$)x≥$\frac{64}{125}$,所以x≤3,因此最多降价3次.…(8分)
点评 本题考查了指数函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
18.下列函数中,既是偶函数又存在零点的是( )
| A. | f(x)=sinx | B. | f(x)=x2+1 | C. | f(x)=lnx | D. | f(x)=cosx |
5.用更相减损术法,计算56和264的最大公约数时,需要做的减法次数是( )
| A. | 5、 | B. | 6 | C. | 7 | D. | 8 |
2.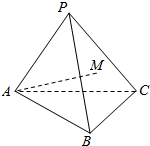 如图,在三棱锥P-ABC中,AB=AC=PB=PC=10,PA=8,BC=12,点M在平面PBC内,且AM=7,设异面直线AM与BC所成角为α,则cosα的最大值为( )
如图,在三棱锥P-ABC中,AB=AC=PB=PC=10,PA=8,BC=12,点M在平面PBC内,且AM=7,设异面直线AM与BC所成角为α,则cosα的最大值为( )
 如图,在三棱锥P-ABC中,AB=AC=PB=PC=10,PA=8,BC=12,点M在平面PBC内,且AM=7,设异面直线AM与BC所成角为α,则cosα的最大值为( )
如图,在三棱锥P-ABC中,AB=AC=PB=PC=10,PA=8,BC=12,点M在平面PBC内,且AM=7,设异面直线AM与BC所成角为α,则cosα的最大值为( )| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{6}{7}$ | D. | $\frac{4\sqrt{3}}{7}$ |
19.设直线l的方向向量是$\overrightarrow{u}$=(-2,2,t),平面α的法向量$\overrightarrow{v}$=(6,-6,12),若直线l⊥平面α,则实数t等于( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
20.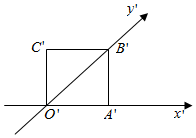 如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
 如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )| A. | 2$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | 2(1+$\sqrt{3}$) | D. | 6 |
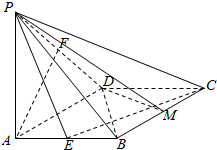 如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB、PD的中点.
如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB、PD的中点.