Question

15．如图，BD=CE，G、H为BC、DE中点，AB=AC，FD=FE，∠BAC=∠DFE．求证：AF∥GH．

Answer 1

分析 如图，AI∥BD，DI∥BA，AK∥CE，KE∥AC，M为BE中点，证明△IDF≌△KEF，故△AIF≌△AKF，所以∠IAF=∠KAF=$\frac{1}{2}$（180-∠B-∠D），而∠MGH=$\frac{1}{2}$（180-∠GMH）=$\frac{1}{2}$（180-∠B-∠D）=∠KAF，所以MG∥EC∥KA即可证明结论．

解答 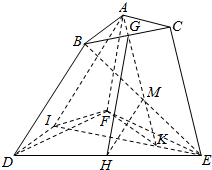证明：如图，AI∥BD，DI∥BA，AK∥CE，KE∥AC，M为BE中点，
因为∠BAC=∠DFE，
所以∠IDF=ID与DF夹角=AB与DF夹角=BC与DE夹角，∠ACB=∠FED，
所以∠FEK=FE与EK夹角=FE与AC夹角=DE与BC夹角．
因此∠IDF=∠FEK．
而ID=BA=CA=KE，DF=EF，
故△IDF≌△KEF，
故△AIF≌△AKF，
所以∠IAF=∠KAF=$\frac{1}{2}$（180-∠B-∠D），
而∠MGH=$\frac{1}{2}$（180-∠GMH）=$\frac{1}{2}$（180-∠B-∠D）=∠KAF，
所以MG∥EC∥KA，
因此GH∥AF．

点评 本题考查两条直线的平行，考查学生分析解决问题的能力，有难度．