题目内容
将双曲线C：x2-y2=1上点绕原点逆时针旋转45°，得到新图形C′，试求C′的方程.
所求的C′方程为xy=
由题意，得旋转变换矩阵
M=
=
，
任意选取双曲线x2-y2=1上的一点P（x0,y0），
它在变换TM作用下变为P′(x′0,y′0),
则有M
=
，故
,
∴
，
又因为点P在曲线x2-y2=1上，所以
-
=1,
即有2
=1.∴所求的C′方程为xy=.
M=
=，任意选取双曲线x2-y2=1上的一点P（x0,y0），
它在变换TM作用下变为P′(x′0,y′0),
则有M
=，故,∴
，又因为点P在曲线x2-y2=1上，所以
-=1,即有2
=1.∴所求的C′方程为xy=.
练习册系列答案
字词句段篇系列答案
相关题目
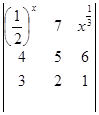中，第3行第2列的元素的代数余子式记作
，
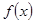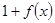的零点属于区间 （ ）
）；
）；
）；
）；
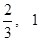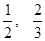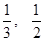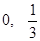绕坐标原点按逆时针方向旋转45°，求所得曲线的方程．
，其中a∈R，若点P（1，1）在矩阵A的变换下得到点P′（0，-3）.（1）求实数a的值；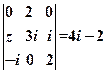
（
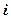为虚数单位），则复数
=_______．
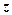三行三列的方阵中有9个数
，
