题目内容
已知 <α<
<α< ,0<β<
,0<β< ,cos(
,cos( +α)=-
+α)=- ,
,
sin( +β)=
+β)= ,求sin(α+β)的值.
,求sin(α+β)的值.
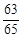
解析试题分析:解:∵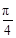 <α<
<α< ,∴
,∴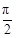 <
<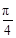 +α<π.
+α<π.
又cos(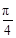 +α)=-
+α)=- ∴sin(
∴sin(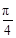 +α)=
+α)=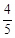 . 3分
. 3分
∵0<β<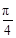 ,∴
,∴ <
< +β<π.又sin(
+β<π.又sin( +β)=
+β)= ,
,
∴cos( +β)=-
+β)=-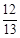 , 6 分
, 6 分
∴sin(α+β)=-sin[π+(α+β)]=-sin[(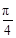 +α)+(
+α)+( +β)]..10分
+β)]..10分
=-[sin(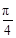 +α)cos(
+α)cos( +β)+cos(
+β)+cos(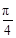 +α)sin(
+α)sin( +β)]……12分
+β)]……12分
=-[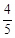 ×(-
×(-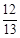 )-
)- ×
× ]=
]=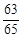 14分
14分
考点:三角函数化简求值
点评:本题中首先找到所求角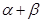 与已知角
与已知角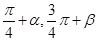 的关系,将所求角用已知角表示出来,然后用整体代入的方法求解
的关系,将所求角用已知角表示出来,然后用整体代入的方法求解

练习册系列答案
相关题目
 三个内角A,B,C所对的边,向量
三个内角A,B,C所对的边,向量 ,设
,设
 ,求角
,求角 ;
; ,求三角形ABC的面积.
,求三角形ABC的面积. 中,内角
中,内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,已知
,已知 .
. 的值;
的值; ,求
,求 为
为 的内角
的内角 的对边,满足
的对边,满足 ,函数
,函数
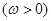 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减. ;
; ,证明
,证明 中,
中,
 的取值范围.
的取值范围. 中,以
中,以 轴为始边,两个锐角
轴为始边,两个锐角 ,
, 的终边分别与单位圆相交于A,B 两点.
的终边分别与单位圆相交于A,B 两点.
 ,
, ,求
,求 的值;
的值; 的终边与单位圆交于
的终边与单位圆交于 点,设角
点,设角 的正弦线分别为
的正弦线分别为 ,试问:以
,试问:以 作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由.
作为三边的长能否构成一个三角形?若能,请加以证明;若不能,请说明理由. ------①
------① ------②
------② ------③
------③ 有
有
 .
. ;
; 的三个内角
的三个内角 满足
满足 ,试判断
,试判断
 的值;
的值; 且
且 ,
, ,求
,求
 的值。
的值。 图像的相邻两条对称轴之间的距离等于
图像的相邻两条对称轴之间的距离等于 。
。 的表达式;(要写出推导过程)
的表达式;(要写出推导过程) 是直角三角形
是直角三角形 的内角,求
的内角,求 的值域。
的值域。