题目内容

2．已知集合A={x|y=lg（2-x）}，集合B=[y|y=$\sqrt{x}$}，则A∩B=[0，2）．

分析 通过求两个函数的定义域和值域化简两个集合、利用交集的定义求出两个集合的交集．

解答 解：A={x|y=lg（2-x）}=（-∞，2），B={y|y=$\sqrt{x}$}=[0，+∞），
则A∩B=[0，2），
故答案为：[0，2）．

点评 本题考查函数定义域的求法：注意求定义域时开偶次方根被开方数大于等于0，对数的真数大于0．利用交集的定义求交集．

练习册系列答案
相关题目
12．设角α是第三象限角，且$|{sin\frac{α}{2}}|=-sin\frac{α}{2}$，则角$\frac{α}{2}$是第四象限角．
13．已知方程$\frac{{x}^{2}}{2+m}$-$\frac{{y}^{2}}{m+1}$=1表示双曲线，则实数m的取值范围是（　　）
A．（-1，∞）B．（-2，-1）C．（-∞，-2）∪（-1，+∞）D．（-∞，-2）
10．直线l过抛物线C：y2=2px（p＞0）的焦点且与x轴垂直，l与C交于A、B两点，P为C的准线上一点，若△ABP的面积为36，则p的值为（　　）
A．3B．6C．12D．6$\sqrt{2}$
17．函数f（x）=（x-a）（x-b）（其中a＞b）的图象如图所示，则函数g（x）=ax+b的大致图象是（　　）
A．B．C．D．
7．已知动点P（x，y）满足5$\sqrt{{（x-1）}^{2}{+（y-2）}^{2}}$=|3x+4y-1|，则点P的轨迹是（　　）
A．直线B．抛物线C．双曲线D．椭圆
14．如图，将正三角形ABC分割成m个边长为1的小正三角形和一个灰色菱形，这个灰色菱形可以分割成n个边长为1的小正三角形．若m：n=47：25，则三角形ABC的边长是（　　）
A．10B．11C．12D．13
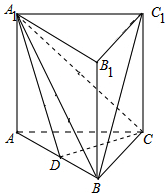11．如图，在三棱柱ABC-A1B1C1中，底面△ABC是边长为2的等边三角形，D为AB中点．
（Ⅰ）求证：BC1∥平面A1CD；
（Ⅱ）若四边形CAA1C1和BAA1B1都是正方形，求多面体CA1C1BD的体积．
12．集合A={x|-2≤x≤3}，B={x|x＜-1}，则A∩（∁RB）等于（　　）
A．{x|x＞-1}B．{x|x≥-1}C．{x|-2≤x≤-1}D．{x|-1≤x≤3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网