题目内容
已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
【解】函数f(x)的定义域为(0,+∞),f′(x)=1- .
.
(1)当a=2时,f(x)=x-2lnx,f′(x)=1-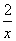 (x>0),
(x>0),
因而f(1)=1,f′(1)=-1,
所以曲线y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x-1),
即x+y-2=0.
(2)由f′(x)=1- =
=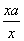 ,x>0知:
,x>0知:
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a.
又当x∈(0,a)时,f′(x)<0;当x∈(a,+∞)时,f′(x)>0,从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-aln a,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.

练习册系列答案
相关题目
近年来,某市为了促进生活垃圾的风分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应分垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(Ⅰ)试估计厨余垃圾投放正确的概率;
(Ⅱ)试估计生活垃圾投放错误额概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为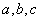 其中a>0,
其中a>0,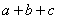 =600。当数据
=600。当数据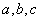 的方差
的方差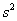 最大时,写出
最大时,写出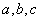 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时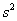 的值。
的值。
(注: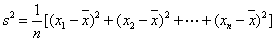 ,其中
,其中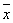 为数据
为数据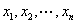 的平均数)
的平均数)
 ,则实数a的取值范围是________.
,则实数a的取值范围是________. sin2x-cos2x,x∈R,若f(x)≥1,则x的取值范围为( )
sin2x-cos2x,x∈R,若f(x)≥1,则x的取值范围为( ) B.
B.
 D.
D.
 的终边过点
的终边过点 .
. 的值;
的值; 的值。
的值。 亦真.
亦真. 那么至少
那么至少 G为△ABC的重心,设
G为△ABC的重心,设 =a,
=a, =b,
=b, =c,则
=c,则 =________(用a,b,c表示).
=________(用a,b,c表示). 的展开式中,各项系数之和为A,各项的二项式系数
的展开式中,各项系数之和为A,各项的二项式系数