题目内容

12．求y=3x+$\frac{4}{x}$（x＜0）的最大值，并求y取最大值时相应的x的值．

分析 由x＜0，变形y=3x+$\frac{4}{x}$=-$（-3x+\frac{4}{-x}）$，利用基本不等式的性质即可得出．

解答 解：∵x＜0，∴y=3x+$\frac{4}{x}$=-$（-3x+\frac{4}{-x}）$≤-$2\sqrt{-3x•\frac{4}{-x}}$=-4$\sqrt{3}$，当且仅当x=-$\frac{2\sqrt{3}}{3}$时取等号．

点评 本题考查了基本不等式的性质，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
2．已知sin（$\frac{π}{4}-α$）=$\frac{\sqrt{2}}{2}$，则cos（$\frac{π}{4}+α$）的值是$\frac{\sqrt{2}}{2}$．
3．全集U=R，若集合A={x|3≤x＜10}，B={x|2＜x≤7}，则
（1）求A∩B，A∪B；
（2）若集合C={x|x＞a}，A⊆C，求a的取值范围．
20．某厂生产的某种产品包括一等品和二等品，如果生产出一件一等品，可获利200元，如果生产出一件二等品则损失100元，已知该厂生产该种产品的过程中，二等品率p与日产量x的函数关系是：p=$\frac{3x}{4x+32}$（x∈N*），问该厂的日产量为多少件时，可获得最大盈利，并求出最大日盈利额．（二等品率p为日产二等品数与日产量的比值）
7．已知向量$\overrightarrow{a}$=（sinθ，1），$\overrightarrow{b}$=（2cosθ，-1），且θ∈（0，π），若$\overrightarrow{a}⊥\overrightarrow{b}$，则θ=（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{2}$D．$\frac{3π}{4}$
2．己知椭圆l0x2+5y2=27，过定点C（2，0）的两条互相垂直的动直线分别交椭圆于P，Q两点，F1，F2分别为左、右焦点，O为坐标原点．
（1）求向量|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|的最值；
（2）当向量$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$与$\overrightarrow{Q{F}_{1}}$+$\overrightarrow{Q{F}_{2}}$互相垂直时，求P，Q两点所在直线方程．
9．双曲线$\frac{x^2}{{25-{m^2}}}$-$\frac{y^2}{{11+{m^2}}}$=1（0＜m＜5）的焦距为（　　）
A．6B．12C．36D．$2\sqrt{14-2{m^2}}$
6．已知偶函数f（x）在区间[0，+∞）上是增函数，则f（-1）与f（2）的大小关系是（　　）
A．f（-1）≥f（2）B．f（-1）≤f（2）C．f（-1）＞f（2）D．f（-1）＜f（2）
7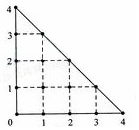．某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获量Y（单位：kg）与它的“相近”作物株数X之间的关系如表所示：
X1234
Y51484542
这里，两株作物“相近”是指它们之间的直线距离不超过1米．
（1）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰好“相近”的概率；
（2）从所种作物中随机选取一株，求它的年收获量Y的分布列．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网