题目内容
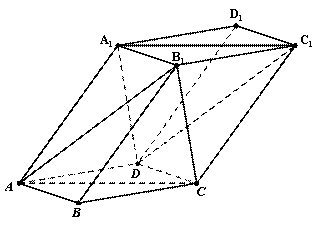
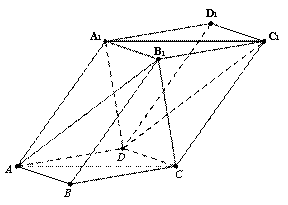
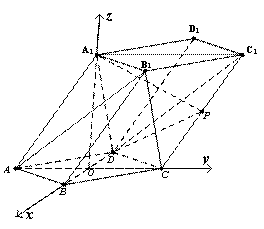
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形
且∠A1AC=∠DAB=60o,平面AA1C1C⊥平面ABCD.(Ⅰ)证明:BD⊥AA1;
(Ⅱ)证明:平面AB1C∥平面DA1C1;
(Ⅲ)在棱CC1上是否存在点P,使得平面PDA1和平面DA1C1所成锐二面角的余弦值为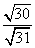 ?若存在,求出点P的位置;若不存在,说明理由.
?若存在,求出点P的位置;若不存在,说明理由.
 |
解:(Ⅰ)证明:连接BD,∵平面ABCD为菱形,
 ∴BD⊥AC,由于平面AA1C1C⊥平面ABCD,
∴BD⊥AC,由于平面AA1C1C⊥平面ABCD,
且交线为AC,则BD⊥平面AA1C1C,
又A1A⊂平面AA1C1C,
故BD⊥AA1.
(Ⅱ)证明:由棱柱的性质
知四边形AB1C1D为平行四边形
∴AB1∥DC1,∵AB1在平面DA1C1外,DC1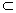 平面DA1C1
平面DA1C1
∴AB1∥平面DA1C1 …
同理B1C∥平面DA1C1…
AB1∩B1C=B1, ∴平面AB1C∥平面DA1C1.
(Ⅲ)设AC交BD于O,连接A1O, ∵菱形AA1C1C且∠A1AC =60o,
∴正三角形A1AC ,且O为AC中点, ∴A1O⊥AC
又平面AA1C1C⊥平面ABCD,平面AA1C1C∩平面ABCD=AC
∴A1O⊥平面ABCD,又BD⊥AC,
如图,以O为坐标原点建立空间直角坐标系,设OB=1
则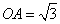 ,
,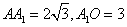 ,
,
 ,
,
 ,
, 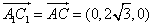
 ,
,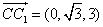
 设
设 则
则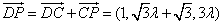
设平面DA1C1和平面PDA1 的的法向量
分别为
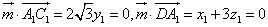 ,
,
取
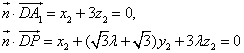
取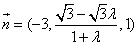

 (舍去)
(舍去)
当P为CC1的中点时,平面PDA1和平面DA1C1所成的锐二面角的余弦值为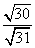 .
.

练习册系列答案
相关题目
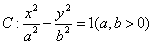 的一条渐近线方程是
的一条渐近线方程是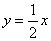 ,它的一个焦点在抛物线
,它的一个焦点在抛物线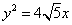 的准线上,点
的准线上,点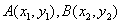 是双曲线
是双曲线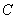 右支上相异两点,且满足
右支上相异两点,且满足
 为线段
为线段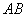 的中点,直线
的中点,直线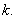
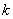 表示点
表示点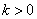 ,
,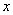 轴于点
轴于点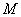 ,直线
,直线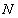 ,求
,求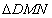 的面积的取值范围.
的面积的取值范围.  中,当离心率e趋近于0,椭圆就趋近于圆,类比圆的面积公式,椭圆C的面积
中,当离心率e趋近于0,椭圆就趋近于圆,类比圆的面积公式,椭圆C的面积 .
.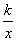 +
+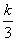 在(1,+∞)上是增函数,则实数k的取值范围是( ).
在(1,+∞)上是增函数,则实数k的取值范围是( ).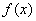 是定义在
是定义在 上的奇函数,当
上的奇函数,当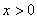 时,
时,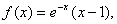 给出以下命题:
给出以下命题:
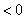 时,
时, ; ②函数
; ②函数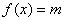 有解,则实数
有解,则实数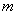 的取值范围是
的取值范围是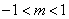 ;
;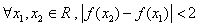 恒成立.
恒成立. 与
与 ,两数的等比中项是( )
,两数的等比中项是( ) C.
C. D.
D.
 B
B (B)
(B)  (C)
(C) (D)
(D) 
 ,则
,则 的最小值是( )
的最小值是( ) (C)5 (D)
(C)5 (D)
 ”的否定是( )
”的否定是( ) B.存在
B.存在 D.对任意的
D.对任意的