题目内容
已知双曲线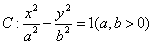 的一条渐近线方程是
的一条渐近线方程是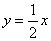 ,它的一个焦点在抛物线
,它的一个焦点在抛物线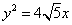 的准线上,点
的准线上,点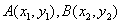 是双曲线
是双曲线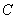 右支上相异两点,且满足
右支上相异两点,且满足
 为线段
为线段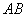 的中点,直线
的中点,直线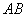 的斜率为
的斜率为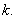
(Ⅰ)求双曲线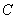 的方程;
的方程;
(Ⅱ)用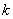 表示点
表示点 的坐标;
的坐标;
(Ⅲ)若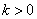 ,
,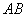 的中垂线交
的中垂线交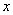 轴于点
轴于点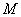 ,直线
,直线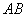 交
交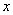 轴于点
轴于点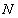 ,求
,求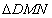 的面积的取值范围.
的面积的取值范围.
解:(Ⅰ)
 双曲线
双曲线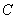 的方程为
的方程为 ; ……………3分
; ……………3分
(Ⅱ)方法一:
设直线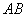 的方程为
的方程为 代入方程
代入方程 得
得
 当
当 时记两个实数根为
时记两个实数根为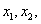
则

∴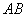 的方程为
的方程为
 把
把 代入得
代入得
 ………… 6分
………… 6分
下求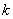 的取值范围:法一:由
的取值范围:法一:由 得
得 即
即
而 所以
所以 化简得
化简得 ………… 7分
………… 7分
法二:在 中令
中令 得
得

即 所以
所以 ………… 7分
………… 7分
方法二: 两式相减得
两式相减得

 ……………6分
……………6分
(Ⅲ)由(Ⅱ)可知方程
 中令
中令 得
得
设点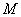 的坐标为
的坐标为 由
由 得
得

∴ …………9分
…………9分

 …… 11分
…… 11分

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 与
与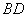 所成的角的度数为 ,当三棱锥的体积取得最大值时, 四棱锥
所成的角的度数为 ,当三棱锥的体积取得最大值时, 四棱锥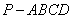 的高
的高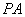 的长为 .
的长为 .
 满足条件
满足条件  时,目标函数
时,目标函数 的最大值是
的最大值是  B.
B. C.
C.  D.
D.
 值为( )
值为( ) B.
B. C.
C. D.
D.

 中,直线
中,直线 (
( )与曲线
)与曲线 及
及 ,则
,则 .
.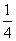 ,且样本容量
,且样本容量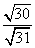 ?若存在,求出点P的位置;若不存在,说明理由.
?若存在,求出点P的位置;若不存在,说明理由.