题目内容
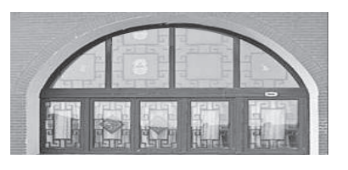
【题目】如下图所示,某窑洞窗口形状上部是圆弧![]() ,下部是一个矩形
,下部是一个矩形![]() ,圆弧
,圆弧![]() 所在圆的圆心为O,经测量
所在圆的圆心为O,经测量![]() 米,
米,![]() 米,
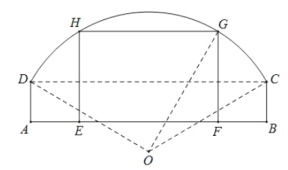
米,![]() ,现根据需要把此窑洞窗口形状改造为矩形
,现根据需要把此窑洞窗口形状改造为矩形![]() ,其中E,F在边
,其中E,F在边![]() 上,G,H在圆弧
上,G,H在圆弧![]() 上.设
上.设![]() ,矩形
,矩形![]() 的面积为S.
的面积为S.
(1)求矩形![]() 的面积S关于变量
的面积S关于变量![]() 的函数关系式;
的函数关系式;
(2)求![]() 为何值时,矩形
为何值时,矩形![]() 的面积S最大?
的面积S最大?
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
(1)结合几何图形计算的直角三角形勾股定理,找出矩形![]() 的面积S关于变量θ的函数关系式;
的面积S关于变量θ的函数关系式;
(2)对S关于变量θ的函数关系式进行求导分析,算出![]() 时的
时的![]() 的值,三角计算即可得出结果.
的值,三角计算即可得出结果.
解:(1)如图,作![]() 分别交
分别交![]() ,
,![]() 于M,N,
于M,N,
由四边形![]() ,
,![]() 是矩形,O为圆心,
是矩形,O为圆心,![]() ,
,
所以![]() ,
,![]() ,P,M,N分别为
,P,M,N分别为![]() ,
,![]() ,
,![]() 中点,
中点,![]() ,
,

在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以 ,
,![]() ,
,
所以S关于![]() 的函数关系式为:
的函数关系式为:![]() ,
,![]()
(2)由(1)得:![]()
因为![]() ,
,
所以![]() ,
,
令![]() ,得
,得![]() ,
,
设![]() ,且
,且![]() ,
,
所以![]() ,得
,得![]() ,即S在
,即S在![]() 单调递增,
单调递增,
![]() ,得
,得![]() ,即S在
,即S在![]() 单调递减
单调递减
所以当![]() 时,S取得最大值,
时,S取得最大值,
所以当![]() 时,矩形
时,矩形![]() 的面积S最大.
的面积S最大.

练习册系列答案
相关题目
