题目内容
 函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<
函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再利用y=Asin(ωx+φ)的图象变换规律,可得结论.
解答:
解:由函数的图象可得
T=
•
=
-
,求得ω=2.
再根据五点法作图可得 2×
+ϕ=π,求得ϕ=
,
故f(x)=sin(2x+
)=sin2(x+
),
故把y=f(x)的图象上所有点向右平移
个单位,可得y=sin[2(x-
)+
]=sin2x的图象,
故答案为:
.
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
再根据五点法作图可得 2×
| π |
| 3 |
| π |
| 3 |
故f(x)=sin(2x+
| π |
| 3 |
| π |
| 6 |
故把y=f(x)的图象上所有点向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
故答案为:
| π |
| 6 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
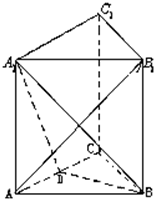 如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
 对一个边长互不相等的凸n(n≥3)边形的边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色.所有不同的染色方法记为P(n),则P(n)=
对一个边长互不相等的凸n(n≥3)边形的边染色,每条边可以染红、黄、蓝三种颜色中的一种,但是不允许相邻的边有相同的颜色.所有不同的染色方法记为P(n),则P(n)=