题目内容
已知函数f(x)=-
+x在区间[m,n]上的值域是[3m,3n],则m-n= .
| x2 |
| 2 |
考点:函数的值域
专题:函数的性质及应用
分析:对m和n的范围进行分类讨论,并根据函数的单调性表示出函数的最大值和最小值建立等式求得m和n.
解答:
解:①当m<n≤1时,函数在区间[m,n]上单调增,
则
,求得m=-4,n=0.
②当1<m<n时,
f(x)在[m,n]上递减,且f(x)<
值域为[3m,3n],
3n<
,矛盾
③m≤1<n时,
f(x)max=
,
若值域为[3m,3n],
则3n=
,n=
与n>1矛盾
综上,符合条件的m,n的值为
m=-4,n=0,
∴m-n=-4,
故答案为:-4
则
|
②当1<m<n时,
f(x)在[m,n]上递减,且f(x)<
| 1 |
| 2 |
值域为[3m,3n],
3n<
| 1 |
| 2 |
③m≤1<n时,
f(x)max=
| 1 |
| 2 |
若值域为[3m,3n],
则3n=
| 1 |
| 2 |
| 1 |
| 6 |
综上,符合条件的m,n的值为
m=-4,n=0,
∴m-n=-4,
故答案为:-4
点评:本题主要考查了二次函数的性质和分类讨论思想的运用.应能熟练掌握二次函数求最值的方法.

练习册系列答案
相关题目
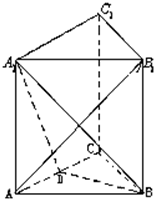 如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
