[题目]已知函数f(1﹣ )的定义域为[1.+∞).则函数y= 的定义域为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知函数f（1﹣ ）的定义域为[1，+∞），则函数y= 的定义域为．

【答案】?
【解析】解：∵函数f（1﹣ ）的定义域为[1，+∞]，
∴f（x）的定义域是[0，1）①，
由（1﹣x）2＞2，解得：x＞1+ 或x＜1﹣ ②，
由①②得函数y= 的定义域是，
所以答案是：．
【考点精析】利用函数的定义域及其求法对题目进行判断即可得到答案，需要熟知求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零．

练习册系列答案

相关题目

【题目】直角△ABC中，∠C=90°，D在BC上，CD=2DB，tan∠BAD= ，则sin∠BAC=（）
A.
B.
C.
D. 或

【题目】如图，在凸四边形ABCD中，AB=1，BC= ，AC⊥DC，CD= AC．设∠ABC=θ．

（1）若θ=30°，求AD的长；
（2）当θ变化时，求BD的最大值．

【题目】如图，在三棱柱中，，，平面ABC．

若，求直线与平面所成的角的大小；

在的条件下，求二面角的大小；

若，平面，G为垂足，令其中p、q、，求p、q、r的值．

【题目】设△ABC的内角A，B，C的对边分别为a、b、c，a=btanA，且B为钝角．
（1）证明：B﹣A= ；
（2）求sinA+sinC的取值范围．

【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣1，其中n∈N* ．
（1）求数列{an}的通项公式；
（2）设anbn= ，求数列{bn}的前n项和为Tn ．

【题目】已知函数为定义域上的奇函数，且在上是单调递增函数，函数，数列为等差数列，，且公差不为0，若，则（）

A. 45 B. 15 C. 10 D. 0

【题目】某工厂有两台不同机器A和B生产同一种产品各10万件，现从各自生产的产品中分别随机抽取20件，进行品质鉴定，鉴定成绩的茎叶图如图所示：

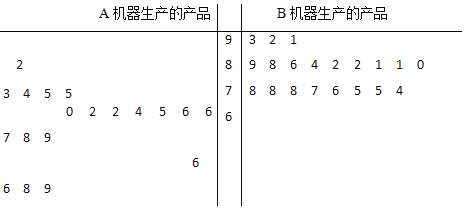
该产品的质量评价标准规定：鉴定成绩达到的产品，质量等级为优秀；鉴定成绩达到的产品，质量等级为良好；鉴定成绩达到的产品，质量等级为合格将这组数据的频率视为整批产品的概率．

Ⅰ从等级为优秀的样本中随机抽取两件，记X为来自B机器生产的产品数量，写出X的分布列，并求X的数学期望；

Ⅱ完成下列列联表，以产品等级是否达到良好以上含良好为判断依据，判断能不能在误差不超过的情况下，认为B机器生产的产品比A机器生产的产品好；

	A生产的产品	B生产的产品	合计
良好以上含良好
合格
合计

已知优秀等级产品的利润为12元件，良好等级产品的利润为10元件，合格等级产品的利润为5元件，A机器每生产10万件的成本为20万元，B机器每生产10万件的成本为30万元；该工厂决定：按样本数据测算，两种机器分别生产10万件产品，若收益之差达到5万元以上，则淘汰收益低的机器，若收益之差不超过5万元，则仍然保留原来的两台机器你认为该工厂会仍然保留原来的两台机器吗？