题目内容
设各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 恰好是等比数列
恰好是等比数列 的前三项.
的前三项.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)记数列 的前
的前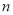 项和为
项和为 ,若对任意的
,若对任意的 ,
,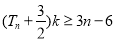 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
题目内容
设各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 恰好是等比数列
恰好是等比数列 的前三项.
的前三项.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)记数列 的前
的前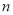 项和为
项和为 ,若对任意的
,若对任意的 ,
,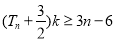 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案