题目内容
已知x与y之间的一组数据:
| x | 0 | 1 | 2 | 3 |
| y | m | 3 | 5.5 | 7 |
已求得y关于x的线性回归方程 =2.1x+0.85,则m的值为( )
=2.1x+0.85,则m的值为( )
A.1 B.0.85
C.0.7 D.0.5
D

郑州市某学校为了促进教师业务能力的提升,决定组织部分学科教师参加市达标课活动,规定用分层抽样的方法,先从语文、英语、政治、历史、地理学科中抽取部分教师参加,各学科教师人数分布表如下:
| 学科 | 语文 | 英语 | 政治 | 历史 | 地理 |
| 人数 | 24 | 24 | 15 | 12 | 9 |
| 抽取人数 | 8 | 8 | a | b | c |
(1)求a、b、c的值;
(2)若要在历史和地理学科已抽取的教师中,随机选取两名教师参加市教学技能竞赛,求抽取的两位教师全是历史教师的概率.
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.
| 序号(i) | 分组(睡眠时间) | 频数(人数) | 频率 |
| 1 | [4,5) | 6 | 0.12 |
| 2 | [5,6) |
| 0.20 |
| 3 | [6,7) | a | |
| 4 | [7,8) | b | |
| 5 | [8,9) |
| 0.08 |
(1)求n的值.若a=20,将表中数据补全,并画出频率分布直方图.
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间[4,5)的中点值是4.5)作为代表.若据此计算的上述数据的平均值为6.52,求a、b的值,并由此估计该学校学生的日平均睡眠时间在7小时以上的概率.
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程为 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性相关系数r和相关指数R2都是描述线性相关强度的量,r和R2越大,相关强度越强.
④在一个2×2列联表中,计算得χ2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
A.0 B.1
C.2 D.3
本题可以参考独立性检验临界值表:
| P(χ2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(χ2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
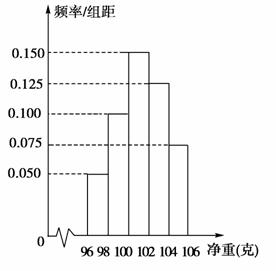
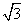 ,BC=4.
,BC=4. ,若DE∥平面PAB,求λ的值.
,若DE∥平面PAB,求λ的值.
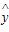 =
=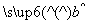 x+
x+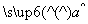 ,则“(x0,y0)满足线性回归方程
,则“(x0,y0)满足线性回归方程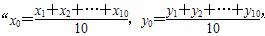 的( )
的( ) B.
B.
 D.
D.