题目内容
由双曲线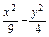
=1上的一点P与左、右两焦点F1、F2构成△PF1F2，求△PF1F2的内切圆与边F1F2的切点坐标.
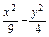=1上的一点P与左、右两焦点F1、F2构成△PF1F2，求△PF1F2的内切圆与边F1F2的切点坐标.N的坐标为（3，0）
由双曲线方程知a=3,b=2,c=
.
如右图，根据从圆外一点引圆的两条切线长相等及双曲线定义可得
|PF1|-|PF2|=2a.
由于|NF1|-|NF2|=|PF1|-|PF2|="2a. " ①
|NF1|+|NF2|="2c. " ②
由①②得|NF1|=
=a+c.
∴|ON|=|NF1|-|OF1|=a+c-c=a=3.
故切点N的坐标为（3，0）.
根据对称性，当P在双曲线左支上时，切点N的坐标为（-3，0）.
.如右图，根据从圆外一点引圆的两条切线长相等及双曲线定义可得
|PF1|-|PF2|=2a.
由于|NF1|-|NF2|=|PF1|-|PF2|="2a. " ①
|NF1|+|NF2|="2c. " ②
由①②得|NF1|=
=a+c.∴|ON|=|NF1|-|OF1|=a+c-c=a=3.
故切点N的坐标为（3，0）.
根据对称性，当P在双曲线左支上时，切点N的坐标为（-3，0）.
练习册系列答案
相关题目
-
=1的一个焦点作x轴的垂线，求垂线与双曲线的交点到两焦点的距离.
∈（0，
），则二次曲线x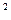
cos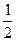
）
）
）
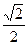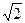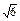，2），求双曲线方程；
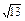，求双曲线方程；
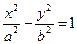(a>0,b>0)的左、右焦点分别为F1、F2,过F1的直线与左支相交于A、B两点.如果|AF2|+|BF2|=2|AB|,那么|AB|=_________.
－
=1的实轴长、虚轴长、焦距成等差数列，则双曲线的离心率是
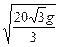千米/秒，其中g为重力加速度，若不计空气阻力与舰高，问舰A发射炮弹的方位角和仰角应是多少？
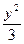=1,过(2,0)的直线被双曲线截得长为6的直线有___________条.
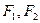是双曲线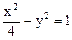
的两个焦点，P在双曲线上，
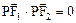，则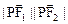
的值等于___________。