题目内容
18.设函数f(x)的定义域为(0,+∞)的增函数,且f(xy)=f(x)+f(y),f(2)=1,则满足f(x)+f(x-3)≤2的x的取值范围是(3,4].分析 令x=y=2,利用f(2)=1即可求得f(4)=2,得f[x(x-3)]≤f(4),再由单调性得到不等式组,解之即可.
解答 解:∵f(2)=1,
∴f(4)=f(2×2)=f(2)+f(2)=2;
∵函数f(x)是定义在(0,+∞)上的增函数,
f(xy)=f(x)+f(y),f(4)=2,
∴f(x)+f(x-3)≤2?f[x(x-3)]≤f(4),
∴$\left\{\begin{array}{l}{x>0}\\{x-3>0}\\{{x}^{2}-3x≤4}\end{array}\right.$,即$\left\{\begin{array}{l}{x>0}\\{x>3}\\{-1≤x≤4}\end{array}\right.$,
解得:3<x≤4.
∴原不等式的解集为:(3,4].
故答案为:(3,4].
点评 本题考查抽象函数及其应用,着重考查赋值法与函数单调性的应用,考查解不等式组的能力,属于中档题.

练习册系列答案
相关题目
6.下列程序框图中,输出的A的值是( )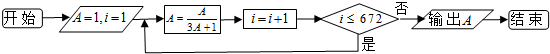
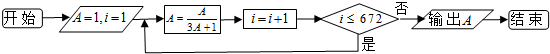
| A. | $\frac{1}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{2017}$ | D. | $\frac{1}{2018}$ |
13.已知坐标原点O(0,0)关于直线L对称的点是M(3,-3),则直线L的方程是( )
| A. | x-2y+1=0 | B. | 2x-y-1=0 | C. | x-y+3=0 | D. | x-y-3=0 |
3.函数f(x)=x3-3x2-x+1在x=x0处取得极大值,设m≠x0,且f(x0)=f(m),则|m-x0|=( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{6}$ |
8.将你手中的笔想放哪就放哪,愿咋放就咋放,总能在教室地面上画一条直线,使之与笔所在的直线( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 垂直 |
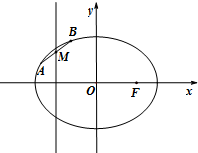 F是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线x=-1上.
F是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线x=-1上.