题目内容
求函数y=sin2x-cos2x的最大值和最小值.
考点:三角函数的最值
专题:计算题,三角函数的图像与性质
分析:利用三角恒等变换,可求得y=
sin(2x-
),从而可求得函数y=sin2x-cos2x的最大值和最小值.
| 2 |
| π |
| 4 |
解答:
解:∵y=sin2x-cos2x
=
(
sin2x-
cos2x)
=
sin(2x-
),
∴当sin(2x-
)=1时,ymax=
,
当sin(2x-
)=-1时,ymin=-
.
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
∴当sin(2x-
| π |
| 4 |
| 2 |
当sin(2x-
| π |
| 4 |
| 2 |
点评:本题考查三角函数的最值,着重考查辅助角公式的应用及正弦函数的最值,属于中档题.

练习册系列答案
相关题目
已知∠B是△ABC的一个内角,下列函数能取负值的是( )
| A、sinB | ||
| B、cosB | ||
C、tan
| ||
D、cos
|
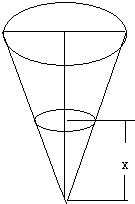 如图,圆锥型量杯口径为2R,高为h,求量杯母线上刻度V(容积)与液面深x的函数关系.
如图,圆锥型量杯口径为2R,高为h,求量杯母线上刻度V(容积)与液面深x的函数关系.