题目内容
6.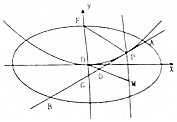 平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.
平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2,抛物线E:x2=2y的准线与椭圆C相切.(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于A,B两点且与抛物线E在第一象限相切于点P,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M,求$\frac{{S}_{△PFG}}{|OG|}$的最小值及此时点P的坐标.
分析 (Ⅰ)运用椭圆的长轴和抛物线的准线,以及椭圆的a,b,c的关系,解得a,b,进而得到椭圆的方程;
(Ⅱ)设P(x0,y0),运用导数求得切线的斜率和方程,令x=0,可得点G的坐标,S△PFG=$\frac{1}{2}$|FG|•|x0|=$\frac{1}{2}$x0•($\frac{1}{2}$+y0)=$\frac{1}{4}$x0(1+x02);$\frac{{S}_{△PFG}}{|OG|}$=$\frac{1}{2}\frac{1+{{x}_{0}}^{2}}{{x}_{0}}=\frac{1}{2}(\frac{1}{{x}_{0}}+{x}_{0})$即可.
解答 解:(Ⅰ)由题意可知2a=2,b=$\frac{1}{2}$,∴椭圆C的方程为:x2+4y2=1.
(Ⅱ)设P(x0,y0),(x0>0)可得${{x}_{0}}^{2}=2{y}_{0}$,由y=$\frac{1}{2}$x2的导数为y′=x,即有切线的斜率为x0,
则切线的方程为y-y0=x0(x-x0),
直线l的方程为y=x0x-y0,令x=0,可得G(0,-y0),
则S△PFG=$\frac{1}{2}$|FG|•|x0|=$\frac{1}{2}$x0•($\frac{1}{2}$+y0)=$\frac{1}{4}$x0(1+x02);
∵|OG|=y0$\frac{{{x}_{0}}^{2}}{2}$,∴$\frac{{S}_{△PFG}}{|OG|}$=$\frac{1}{2}\frac{1+{{x}_{0}}^{2}}{{x}_{0}}=\frac{1}{2}(\frac{1}{{x}_{0}}+{x}_{0})$≥1,
当且仅当x0=1时,即P(1,$\frac{1}{2}$)时,$\frac{{S}_{△PFG}}{|OG|}$有最小值1.
点评 本题考查椭圆的方程的求法,考查抛物线的切线,及三角形的面积的计算,以及化简整理的运算能力,属于中档题题.

| A. | nxn-1e-x | B. | xne-x | C. | 2xne-x | D. | (n-x)xn-1e-x |
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
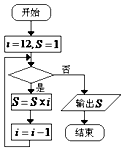
| A. | i≥9 | B. | i≤9 | C. | i≤10 | D. | i≥10 |
| A. | 1 | B. | -1 | C. | -i | D. | i |
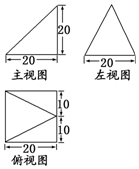 已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.
已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.