题目内容
(12分)已知过点 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
.
(1)求证:当 与
与 垂直时,
垂直时, 必过圆心
必过圆心 ;
;
(2)当 时,求直线
时,求直线 的方程;
的方程;
(3)探索 是否与直线
是否与直线 的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
.(1)求证:当
 与
与 垂直时,
垂直时, 必过圆心
必过圆心 ;
;(2)当
 时,求直线
时,求直线 的方程;
的方程;(3)探索
 是否与直线
是否与直线 的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
的倾斜角有关,若无关,请求出其值;若有关,请说明理由.解:(1)∵ 与
与 垂直,且
垂直,且 ,∴
,∴ ,
,
故直线 方程为
方程为 ,即
,即 ………2分
………2分
∵圆心坐标(0,3)满足直线 方程,
方程,
∴当 与
与 垂直时,
垂直时, 必过圆心
必过圆心 ………………… …4分
………………… …4分
(2)①当直线 与
与 轴垂直时, 易知
轴垂直时, 易知 符合题意
符合题意
②当直线 与
与 轴不垂直时,
轴不垂直时,
设直线 的方程为
的方程为 ,即
,即 ,
,
∵ ,∴
,∴ ,
,
则由 ,得
,得 , ∴直线
, ∴直线 :
: .
.
故直线 的方程为
的方程为 或
或 ………………………………………8分
………………………………………8分
(3)∵ ,∴
,∴ 
① 当 与
与 轴垂直时,易得
轴垂直时,易得 ,则
,则 ,又
,又 ,
,
∴
当 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 ,
,
则由 ,得
,得 (
(
 ),则
),则
∴ =
=
综上所述, 与直线
与直线 的斜率无关,且
的斜率无关,且 .…………………12分
.…………………12分
 与
与 垂直,且
垂直,且 ,∴
,∴ ,
,故直线
 方程为
方程为 ,即
,即 ………2分
………2分∵圆心坐标(0,3)满足直线
 方程,
方程,∴当
 与
与 垂直时,
垂直时, 必过圆心
必过圆心 ………………… …4分
………………… …4分(2)①当直线
 与
与 轴垂直时, 易知
轴垂直时, 易知 符合题意
符合题意②当直线
 与
与 轴不垂直时,
轴不垂直时, 设直线
 的方程为
的方程为 ,即
,即 ,
,∵
 ,∴
,∴ ,
,则由
 ,得
,得 , ∴直线
, ∴直线 :
: .
. 故直线
 的方程为
的方程为 或
或 ………………………………………8分
………………………………………8分(3)∵
 ,∴
,∴ 
① 当
 与
与 轴垂直时,易得
轴垂直时,易得 ,则
,则 ,又
,又 ,
,∴

当
 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为 ,
,则由
 ,得
,得 (
(
 ),则
),则
∴
 =
=
综上所述,
 与直线
与直线 的斜率无关,且
的斜率无关,且 .…………………12分
.…………………12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
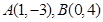 的圆
的圆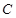 与圆
与圆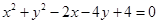 相交,它们的公共弦平行于直线
相交,它们的公共弦平行于直线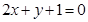 .
.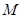 经过一定点
经过一定点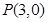 ,且与圆
,且与圆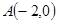 ,动点
,动点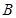 是圆
是圆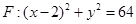 (
(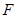 为圆心)上一点,线段
为圆心)上一点,线段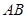 的垂直平分线交
的垂直平分线交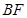 于点
于点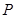 .
. 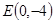 的直线
的直线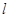 交
交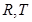 ,且满足
,且满足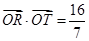 (
(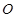 为原点).若存在,求直线
为原点).若存在,求直线
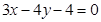 被圆
被圆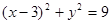 截得的弦长是( )
截得的弦长是( )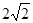
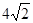
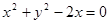 外切且与直线
外切且与直线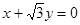 相切于点
相切于点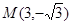 的圆的方程.
的圆的方程.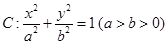 的离心率为
的离心率为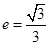 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线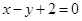 相切,
相切,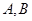 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点, 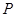 为椭圆
为椭圆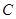 上的动点.
上的动点.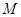 为过
为过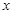 轴的直线上的点,若
轴的直线上的点,若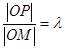 ,求点
,求点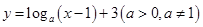 的图像恒过定点
的图像恒过定点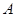 ,过点
,过点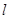 与圆
与圆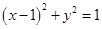 相切,则直线
相切,则直线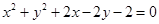 的圆心到直线
的圆心到直线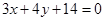 的距离是____________
的距离是____________ 在直线
在直线 上,过点
上,过点 与曲线
与曲线 只有一个公共点
只有一个公共点 ,则
,则 的最小值为__________.
的最小值为__________.