题目内容
已知定点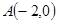 ,动点
,动点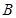 是圆
是圆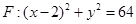 (
(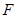 为圆心)上一点,线段
为圆心)上一点,线段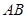 的垂直平分线交
的垂直平分线交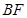 于点
于点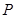 .
.
(I)求动点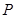 的轨迹方程;
的轨迹方程;
(II)是否存在过点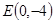 的直线
的直线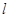 交
交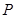 点的轨迹于点
点的轨迹于点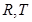 ,且满足
,且满足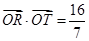 (
(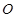 为原点).若存在,求直线
为原点).若存在,求直线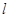 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
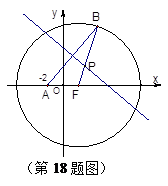
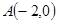 ,动点
,动点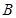 是圆
是圆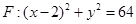 (
(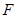 为圆心)上一点,线段
为圆心)上一点,线段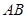 的垂直平分线交
的垂直平分线交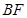 于点
于点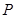 .
. (I)求动点
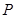 的轨迹方程;
的轨迹方程;(II)是否存在过点
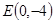 的直线
的直线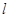 交
交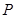 点的轨迹于点
点的轨迹于点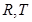 ,且满足
,且满足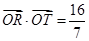 (
(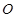 为原点).若存在,求直线
为原点).若存在,求直线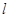 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)由题意得|PA|=|PB|且|PB|+|PF|="r=8." 故|PA|+|PF|=8>|AF|=4
∴P点轨迹为以A、F为焦点的椭圆.……………3分
设椭圆方程为
 . ……………… 6分
. ……………… 6分
(2)假设存在满足题意的直线L.易知当直线的斜率不存在时, 不满足题意.
不满足题意.
故设直线L的斜率为 .
.
 ………………………………7分
………………………………7分
 ………………………8分
………………………8分
 ……………………①.
……………………①.
 …………………10分
…………………10分
 ……………9分
……………9分

 …②.
…②.
由①、②解得
 ………………11分
………………11分

∴P点轨迹为以A、F为焦点的椭圆.……………3分
设椭圆方程为

 . ……………… 6分
. ……………… 6分(2)假设存在满足题意的直线L.易知当直线的斜率不存在时,
 不满足题意.
不满足题意.故设直线L的斜率为
 .
. ………………………………7分
………………………………7分 ………………………8分
………………………8分 ……………………①.
……………………①. …………………10分
…………………10分 ……………9分
……………9分
 …②.
…②.由①、②解得

 ………………11分
………………11分
略

练习册系列答案
相关题目
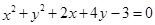 上,且到直线
上,且到直线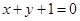 的距离为
的距离为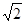 的点共有( )
的点共有( )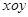 中,已知“葫芦”曲线
中,已知“葫芦”曲线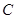 由圆弧
由圆弧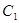 与圆弧
与圆弧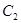 相接而成,两相接点
相接而成,两相接点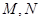 均在直线
均在直线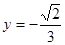 上.圆弧
上.圆弧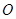 ,半径为
,半径为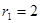 ;圆弧
;圆弧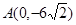 .
.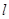 :
: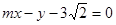 与“葫芦”曲线
与“葫芦”曲线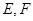 两点.当
两点.当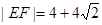 时,求直线
时,求直线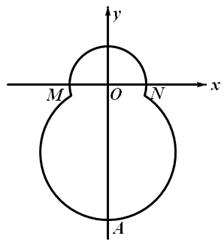
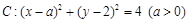 及直线
及直线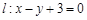 . 当直线
. 当直线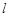 被圆
被圆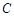 截得的弦长为
截得的弦长为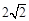 时,
时,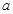 的值;
的值; 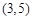 并与圆
并与圆 的动直线
的动直线 与圆
与圆 :
: 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于 .
. 时,求直线
时,求直线 是否与直线
是否与直线 所经过的定点F,直线
所经过的定点F,直线 :
: 与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点.
与x轴的交点是圆C的圆心,圆C恰好经过坐标原点O,设G是圆C上任意一点. 交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长; ?若存在,求出点P坐标;若不存在,请说明理由.
?若存在,求出点P坐标;若不存在,请说明理由.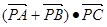 的值是 。
的值是 。