题目内容
已知关于 的一元二次函数
的一元二次函数 ,设集合
,设集合 ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为 和
和
(1)求函数 有零点的概率;
有零点的概率;
(2)求函数 在区间
在区间 上是增函数的概率。
上是增函数的概率。
(1)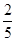 (2)
(2)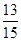
解析试题分析:分别从集合 和
和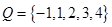 中随机取一个数作为
中随机取一个数作为 和
和 ,共有15种基本情况,逐一列出如下
,共有15种基本情况,逐一列出如下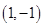 ,
, ,
,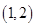 ,
, ,
,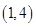 ,
,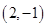 ,
,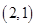 ,
, ,
,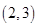 ,
,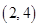 ,
,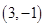
 ,
, ,
,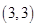 ,
, ;由于是随机取的,每个结果出现的可能性是相等的,符合古典概型的特征;
;由于是随机取的,每个结果出现的可能性是相等的,符合古典概型的特征;
(1)函数 有零点,
有零点,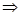
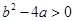 统计出符合条件的数对的个数,既可求出相应的概率值.
统计出符合条件的数对的个数,既可求出相应的概率值.
(2)因为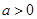 ,一元二次函数
,一元二次函数 的图象抛物线开口向上,对称轴是
的图象抛物线开口向上,对称轴是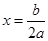 ,
,
由函数 在区间
在区间 上是增函数,知
上是增函数,知 统计出符合条件的数对的个数,既可求出相应的概率值.
统计出符合条件的数对的个数,既可求出相应的概率值.
试题解析: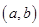 共有
共有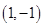 ,
, ,
,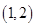 ,
, ,
,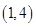 ,
,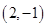 ,
,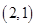 ,
, ,
,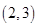 ,
,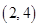 ,
,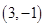
 ,
, ,
,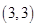 ,
, ,15种情况
,15种情况
(1)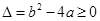 有
有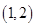 ,
, ,
,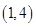 ,
,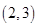 ,
,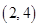 ,
, 六种情况,
六种情况,
所以函数 有零点的概率为
有零点的概率为 ;
;
(2)对称轴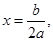 则
则 有
有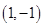 ,
,  ,
,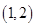
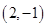 ,
,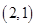 ,
, ,
,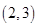 ,
,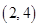 ,
,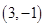
 ,
, ,
,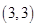 ,
, 13种情况,函数
13种情况,函数 在区间上是增函数的概率为
在区间上是增函数的概率为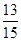
考点:1、古典概型;2、一元二次函数与一元二次方程.

练习册系列答案
相关题目
 ,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a). .
. ),f(
),f( )是否成等比数列,并证明f(
)是否成等比数列,并证明f( 为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围. .
.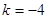 时,求函数
时,求函数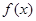 在
在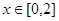 上的值域;
上的值域; ,若存在
,若存在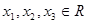 ,使得以
,使得以 为三边长的三角形不存在,求实数
为三边长的三角形不存在,求实数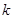 的取值范围.
的取值范围. 且
且 ,求函数
,求函数 的单调区间.
的单调区间. ,
,
 ,函数
,函数 的图像与直线
的图像与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
. 的值;
的值;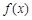 在
在 上的单调递增区间.
上的单调递增区间. 的定义域为E,值域为F.
的定义域为E,值域为F. 与集合F的关系;
与集合F的关系; },求实数a的值.
},求实数a的值. ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值. 定义在(―1,1)上,对于任意的
定义在(―1,1)上,对于任意的 ,有
,有 ,且当
,且当 时,
时, 。
。 是否满足这些条件;
是否满足这些条件; ,求方程
,求方程 的解。
的解。