题目内容
已知向量 ,
,
 ,函数
,函数 的图像与直线
的图像与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
.
(1)求 的值;
的值;
(2)求函数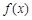 在
在 上的单调递增区间.
上的单调递增区间.
(1) ;(2)
;(2) .
.
解析试题分析:(1)先由向量数量积的坐标运算及倍角公式、两角和差公式得到
 ,再由图像与直线
,再由图像与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 ,得
,得 ,再由最小正周期的计算公式
,再由最小正周期的计算公式 得出
得出 ;(2)由
;(2)由 得
得 ,再由余弦函数的单调性可得
,再由余弦函数的单调性可得 的单调增区间为
的单调增区间为 .
.
试题解析:(1) 1分
1分


 5分
5分
由题意, ,
, ,
, 6分
6分
(2) ,
,
由 得
得
故 时,
时, 单调递增 9分
单调递增 9分
即 的单调增区间为
的单调增区间为 12分.
12分.
考点:1.向量的数量积;2.三角恒等变换;3.三角函数的单调性.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意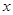 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。 是否具有“
是否具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 上有最大值;
上有最大值; 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若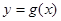 与
与 交点个数为2013,求
交点个数为2013,求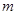 的值.
的值. 的一元二次函数
的一元二次函数 ,设集合
,设集合 ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为 和
和
 有零点的概率;
有零点的概率; 上是增函数的概率。
上是增函数的概率。 .
. 的图像;
的图像; ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.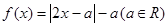 ,不等式
,不等式 的解集为
的解集为 .
. 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
, .
. 的值;
的值; 的值域.
的值域.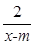 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围.
 ,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.
,若关于x的方程2[f(x)]2-(2a+3)·f(x)+3a=0有五个不同的实数解,求a的取值范围.