题目内容
设函数 的定义域为E,值域为F.
的定义域为E,值域为F.
(1)若E={1,2},判断实数λ=lg22+lg2lg5+lg5﹣ 与集合F的关系;
与集合F的关系;
(2)若E={1,2,a},F={0, },求实数a的值.
},求实数a的值.
(3)若 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.
(1) ;(2)
;(2) 或
或 ;(3)
;(3) .
.
解析试题分析:(1)将定义域的两个值代入求出值域 ,并化简
,并化简 ,判定元素与集合的关系;
,判定元素与集合的关系;
(2)令 或
或 ,解出
,解出 值,根据集合元素的互异性,求出
值,根据集合元素的互异性,求出 值.
值.
(3)先根据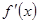 判定函数的单调性,然后讨论
判定函数的单调性,然后讨论 或
或 时,定义域的端点和值域的端点的对应关系问题,从而列出方程组求解.
时,定义域的端点和值域的端点的对应关系问题,从而列出方程组求解.
试题解析:解:(1)∵ ,∴当x=1时,f(x)=0;当x=2时,f(x)=
,∴当x=1时,f(x)=0;当x=2时,f(x)= ,
,
∴F={0, }.
}.
∵λ=lg22+lg2lg5+lg5﹣16 =lg2(lg2+lg5)+lg5﹣
=lg2(lg2+lg5)+lg5﹣ =lg2+lg5﹣
=lg2+lg5﹣ =lg10﹣
=lg10﹣ =
= .
.
∴λ∈F. (5分)
(2)令f(a)=0,即 ,a=±1,取a=﹣1;
,a=±1,取a=﹣1;
令f(a)= ,即
,即 ,a=±2,取a=﹣2,
,a=±2,取a=﹣2,
故a=﹣1或﹣2. (9分)
(3)∵ 是偶函数,且f'(x)=
是偶函数,且f'(x)= >0,
>0,
则函数f(x)在(﹣∞,0)上是减函数,在(0,+∞)上是增函数.
∵x≠0,∴由题意可知: 或0<
或0< .
.
若 ,则有
,则有 ,即
,即 ,
,
整理得m2+3m+10=0,此时方程组无解;
若0< ,则有
,则有 ,即
,即 ,
,
∴m,n为方程x2﹣3x+1=0,的两个根.∵0< ,∴m>n>0,
,∴m>n>0,
∴m= ,n=
,n= . (16分)
. (16分)
考点:1.函数的定义域与值域的关系;2.函数的单调性与最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为多少时,体积V最大?最大值是多少?
为多少时,体积V最大?最大值是多少?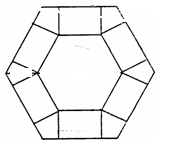
 的一元二次函数
的一元二次函数 ,设集合
,设集合 ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为 和
和
 有零点的概率;
有零点的概率; 上是增函数的概率。
上是增函数的概率。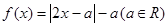 ,不等式
,不等式 的解集为
的解集为 .
. 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
, .
. 的值;
的值; 的值域.
的值域.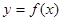 的定义域为
的定义域为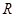 ,若存在常数
,若存在常数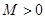 ,使得
,使得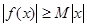 对一切实数
对一切实数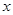 均成立,则称
均成立,则称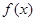 为“圆锥托底型”函数.
为“圆锥托底型”函数.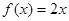 ,
,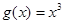 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.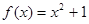 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出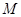 的最大值.
的最大值.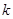 、
、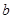 满足什么条件,
满足什么条件,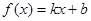 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.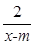 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围.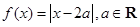 .
.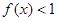 的解集为
的解集为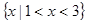 ,求
,求 的值;
的值;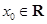 ,使
,使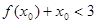 ,求
,求