题目内容
15．若直线l：y=$\sqrt{3}$x与圆C：x2-4x+y2=0相交于A，B两点，则弦长|AB|=（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
分析 先求出圆心到直线的距离，再利用弦长公式求得|AB|的值．
解答 解：圆C：x2-4x+y2=0，可化为：（x-2）2+y2=4
∴圆心坐标为（2，0），半径为2，
∴圆心到直线l：y=$\sqrt{3}$x的距离为d=$\frac{2\sqrt{3}}{\sqrt{3+1}}$=$\sqrt{3}$，
故弦长|AB|=2$\sqrt{4-3}$=2
故选：C．
点评 本题主要考查直线和圆相交的性质，点到直线的距离公式、弦长公式的应用，属于基础题．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
16．设a=22.5，b=log${\;}_{\frac{1}{2}}$2.5，c=（$\frac{1}{2}$）2.5，则a，b，c之间的大小关系是（ ）
| A． | c＞b＞a | B． | c＞a＞b | C． | a＞c＞b | D． | b＞a＞c |
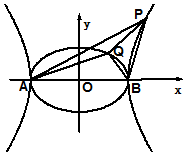已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点，P、Q分别为双曲线和椭圆上不同于两点A、B的动点，且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ（$\overrightarrow{OA}$+$\overrightarrow{QB}$）（λ∈R，|λ|＞1），设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4，则k1+k2+k3+k4的值（ ）